Salut,
Voila j'ai quelque problème sur quelque exercices , tel que celui ci :
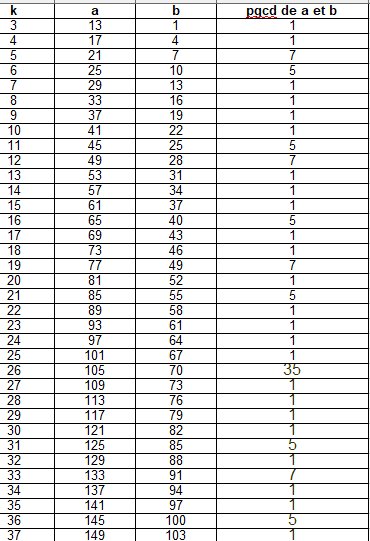
k est un entier naturel supérieur ou égal à 3. On pose a=4k+1 et b=3k-8
Quels sont les diviseurs positifs communs à a et b.
Exercice spé Math Term S
13 messages
- Page 1 sur 1
Re: Exercice spé Math Term S
salut
On montre facilement qu'un diviseur commun à a et b appartient à l'ensemble {1;5;7;35}
Pour être plus précis, le résultat dépend de la valeur de k et ça se complique un peu !
On montre facilement qu'un diviseur commun à a et b appartient à l'ensemble {1;5;7;35}
Pour être plus précis, le résultat dépend de la valeur de k et ça se complique un peu !
Re: Exercice spé Math Term S
Bonjour
Comme très souvent on exploite : les diviseurs communs à a et b sont les diviseurs de leur PGCD.
On ne connait pas ce PGCD , mais en appliquant la propriété PGCD(a,b) = PGCD(a-t.b,b) , deux fois,
on trouve PGCD(a,b) = PGCD(u(k),35).
Il ne reste qu'a déterminer u(k) et la fin est facile.
Bon courage
Comme très souvent on exploite : les diviseurs communs à a et b sont les diviseurs de leur PGCD.
On ne connait pas ce PGCD , mais en appliquant la propriété PGCD(a,b) = PGCD(a-t.b,b) , deux fois,
on trouve PGCD(a,b) = PGCD(u(k),35).
Il ne reste qu'a déterminer u(k) et la fin est facile.
Bon courage
Re: Exercice spé Math Term S
Il ne reste qu'à déterminer, bien sûr...je n'ai pas trouvé comment corriger !
Re: Exercice spé Math Term S
Bonjour;
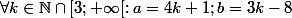 .
.
Soit un diviseur commun de
un diviseur commun de  et
et  ; donc
; donc  est aussi un diviseur de
est aussi un diviseur de 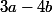 .
.
On a :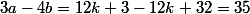 ; donc
; donc  est un diviseur de
est un diviseur de 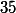 ; donc :
; donc : 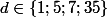 .
.
Si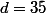 ; donc
; donc \in\mathbb N\end {matrix})
\in\mathbb N\end {matrix})
\in\{(-1-4t;-9-35t);t\in\mathbb Z^{*-}\}\\\\(k;f)\in\{(-9-35t;-1-3t);t\in\mathbb Z^{*-}\} \end {matrix})
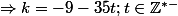 ;
;
donc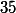 est un diviseur commun de
est un diviseur commun de  et
et  si
si 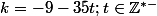 ;
;
donc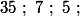 et
et  sont les diviseurs communs de
sont les diviseurs communs de  et
et  si
si 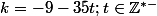 ;
;
sinon , si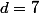 ; donc
; donc \in\mathbb N\end {matrix})
\in\mathbb N\end {matrix})
\in\{(-1-4t;-2-7t);t\in\mathbb Z^{*-}\}\\\\(k;f)\in\{(-2-7t;-1-3t);t\in\mathbb Z^{*-}\} \end {matrix})
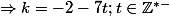 ;
;
donc est un diviseur commun de
est un diviseur commun de  et
et  si
si 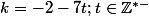 ;
;
donc et
et  sont les diviseurs communs de
sont les diviseurs communs de  et
et  si
si 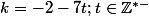 ;
;
sinon , si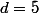 ; donc
; donc \in\mathbb N\end {matrix})
\in\mathbb N\end {matrix})
\in\{(1-4t;1-5t);t\in\mathbb Z^{*-}\}\\\\(k;f)\in\{(1-5t;-1-3t);t\in\mathbb Z^{*-}\} \end {matrix})
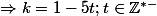 ;
;
donc est un diviseur commun de
est un diviseur commun de  et
et  si
si 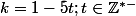 ;
;
donc et
et  sont les diviseurs communs de
sont les diviseurs communs de  et
et  si
si 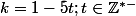 ;
;
sinon est le seul diviseur commun de
est le seul diviseur commun de  et
et  , et dans ce cas a et b sont premiers entre-eux .
, et dans ce cas a et b sont premiers entre-eux .
Conclusion :
Si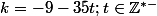 ; alors
; alors 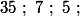 et
et  sont les diviseurs communs de
sont les diviseurs communs de  et
et  ;
;
sinon si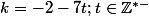 ; alors
; alors  et
et  sont les diviseurs communs de
sont les diviseurs communs de  et
et  ;
;
sinon si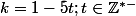 ; alors
; alors  et
et  sont les diviseurs communs de
sont les diviseurs communs de  et
et  .
.
sinon et
et  sont premiers entre-eux .
sont premiers entre-eux .
Soit
On a :
Si
donc
donc
sinon , si
donc
donc
sinon , si
donc
donc
sinon
Conclusion :
Si
sinon si
sinon si
sinon
Modifié en dernier par aymanemaysae le 13 Nov 2018, 10:32, modifié 1 fois.
Re: Exercice spé Math Term S
aymanemaysae a écrit:
Conclusion :
Si; alors
et
sont les diviseurs communs de
et
.
Si; alors
et
sont les diviseurs communs de
et
.
Si; alors
et
sont les diviseurs communs de
et
.
Autrement , a et b sont premiers entre-eux .
Bonjour
Quelques petites choses à régler:
Dans le second cas, si t=-4 , c'est-à-dire k=-2-7*(-4)=26, alors les diviseurs communs à a et b sont les éléments de {1;5;7;35}
Re: Exercice spé Math Term S
Bonjour à tous
Ne trouvez vous pas plus facile d'exploiter PGCD(4k+1,3k-8) = PGCD(k+9,35) ?
Cordialement
Ne trouvez vous pas plus facile d'exploiter PGCD(4k+1,3k-8) = PGCD(k+9,35) ?
Cordialement
Re: Exercice spé Math Term S
Bonjour;
Merci Mathelot pour la remarque : je crois que j'ai rectifié mon erreur .
Merci Mathelot pour la remarque : je crois que j'ai rectifié mon erreur .
Re: Exercice spé Math Term S
Rdvn a écrit:Bonjour
Comme très souvent on exploite : les diviseurs communs à a et b sont les diviseurs de leur PGCD.
On ne connait pas ce PGCD , mais en appliquant la propriété PGCD(a,b) = PGCD(a-t.b,b) , deux fois,
on trouve PGCD(a,b) = PGCD(u(k),35).
Il ne reste qu'a déterminer u(k) et la fin est facile.
Bon courage
J'ai essayer d'utiliser le PGCD (chapitre que j'ai pas abordé en classe mais que je fais de mon côté)
j'ai fait
a=4k+1
b=3k-8
3a-4b=35
PGCD(a;b)=PGCD(a;35) par rapport a une propriété que j'ai vue dans mon livre
sauf que normalement le PGCD de a et 35 sont le produit des facteurs premier communs de a et 35 mais il en on pas.
a=3(n+1)
35=7*5
aymanemaysae a écrit:Bonjour;.
Soitun diviseur commun de
et
; donc
est aussi un diviseur de
.
On a :; donc
est un diviseur de
; donc :
.
Si; donc
\in\mathbb N\end {matrix})
\in\mathbb N\end {matrix})
\in\{(-1-4t;-9-35t);t\in\mathbb Z^{*-}\}\\\\(k;f)\in\{(-9-35t;-1-3t);t\in\mathbb Z^{*-}\} \end {matrix})
;
doncest un diviseur commun de
et
si
;
doncet
sont les diviseurs communs de
et
si
;
sinon , si; donc
\in\mathbb N\end {matrix})
\in\mathbb N\end {matrix})
\in\{(-1-4t;-2-7t);t\in\mathbb Z^{*-}\}\\\\(k;f)\in\{(-2-7t;-1-3t);t\in\mathbb Z^{*-}\} \end {matrix})
;
doncest un diviseur commun de
et
si
;
doncet
sont les diviseurs communs de
et
si
;
sinon , si; donc
\in\mathbb N\end {matrix})
\in\mathbb N\end {matrix})
\in\{(1-4t;1-5t);t\in\mathbb Z^{*-}\}\\\\(k;f)\in\{(1-5t;-1-3t);t\in\mathbb Z^{*-}\} \end {matrix})
;
doncest un diviseur commun de
et
si
;
doncet
sont les diviseurs communs de
et
si
;
sinonest le seul diviseur commun de
et
, et dans ce cas a et b sont premiers entre-eux .
Conclusion :
Si; alors
et
sont les diviseurs communs de
et
;
sinon si; alors
et
sont les diviseurs communs de
et
;
sinon si; alors
et
sont les diviseurs communs de
et
.
sinonet
sont premiers entre-eux .
merci pour la réponse mais je pense que le raisonnement est peut être trop complexe comparé à ce que l'on attend de moi, j'ai d'ailleurs un peu de mal à le saisir
Re: Exercice spé Math Term S
Bonsoir,
Je reprend ma réponse précédente (a et b entiers, strictement positifs):
Comme très souvent on exploite : les diviseurs communs à a et b sont les diviseurs de leur PGCD.
On ne connait pas ce PGCD , mais on va utiliser la propriété PGCD(a,b) = PGCD(a-t.b,b) , t entier relatif, pour trouver une forme plus facile à manipuler :
PGCD(4k+1 , 3k-8)=PGCD(4k+1-(3k-8) , 3k-8)=PGCD(k+9 , 3k-8) puis
PGCD(3k-8 , k+9)=PGCD(3k-8-3(k+9) , k+9)=PGCD(-35 , k+9)=PGCD(k+9 , 35)
on rassemble les égalités :
PGCD(4k+1 , 3k-8)=PGCD(k+9 , 35)
Donc un entier divise 4k+1 et 3k-8 si et seulement si il divise 35 et k+9 , ce qui dépend de k , bien sûr.
Les diviseurs positifs de 35 sont 1 , 5 , 7 , 35 . La fin est facile.
Remarque : était ce un exercice proposé en classe ? Si oui je n'en vois pas l'utilité si le PGCD n'a pas été étudié,
car c'est typiquement une situation où l'usage du PGCD simplifie largement le problème.
Bon courage
Je reprend ma réponse précédente (a et b entiers, strictement positifs):
Comme très souvent on exploite : les diviseurs communs à a et b sont les diviseurs de leur PGCD.
On ne connait pas ce PGCD , mais on va utiliser la propriété PGCD(a,b) = PGCD(a-t.b,b) , t entier relatif, pour trouver une forme plus facile à manipuler :
PGCD(4k+1 , 3k-8)=PGCD(4k+1-(3k-8) , 3k-8)=PGCD(k+9 , 3k-8) puis
PGCD(3k-8 , k+9)=PGCD(3k-8-3(k+9) , k+9)=PGCD(-35 , k+9)=PGCD(k+9 , 35)
on rassemble les égalités :
PGCD(4k+1 , 3k-8)=PGCD(k+9 , 35)
Donc un entier divise 4k+1 et 3k-8 si et seulement si il divise 35 et k+9 , ce qui dépend de k , bien sûr.
Les diviseurs positifs de 35 sont 1 , 5 , 7 , 35 . La fin est facile.
Remarque : était ce un exercice proposé en classe ? Si oui je n'en vois pas l'utilité si le PGCD n'a pas été étudié,
car c'est typiquement une situation où l'usage du PGCD simplifie largement le problème.
Bon courage
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :