Courbes et dérivation

[iris75]

Bonjour , je bloque sur mon second exercice qui est :

Soit la fonction f définie sur R par f(x) = 4 - x^2 et la fonction g définie sur R \ [0] par g(x) = 1 + 2/x

1. Les courbes Cf et Cg semble avoir une même tangente T commune. En quel point A ?

2. Démontrer la conjecture précédente puis déterminer une équation de la tangente T

J’y suis depuis deux bonnes heures et je ne réussis toujours pas à avancer ne serait ce qu’un peu. Merci de me débloquer ☹️

[capitaine nuggets]

Salut !

La première question ne semble être qu'une simple observation graphiques des courbes représentatives des fonctions et . Il suffit juste d'observer donc. Si les courbes ne sont pas données dans l'exercice, as-tu pensé à les tracer sur ta calculatrice ou sur géogébra par exemple ?

Pour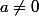 , quelle est l'équation de la tangente à au point d'abscisse ? Quelle est l'équation de la tangente à au point d'abscisse ?

[pascal16]

si tu prends a pour f, prends b pour g, c'est ça l'astuce, il faut être capable de différencier le point de contact de la tangente avec chacune des deux courbes.


NB : soit une tangente à la courbe de g, elle est tangente à f quand elle ne la coupe qu'en un seul point limite. Çà rappelle une propriété du delta des équations du second degré...

[iris75]

Justement ma calculatrice c’est une Casio et je n’arrive pas à faire cela et je ne comprend vraiment pas ce que vous me dites

[pascal16]

le tracé aide beaucoup en effet

le point d'abscisse 1 te parait-il particulier ?

[iris75]

Je sais pas puisque je ne visualise rien je n’ai pas de graphique

[Ben314]

Salut,
Ben dans ce cas, utilise géogébra (en ligne) ou n'importe quel traceur de courbe sur le net (y'en a des tonnes...) :
https://www.geogebra.org/graphing
Dans la fenêtre "saisie" (à gauche), tu rentre tes équations de fonctions sous la forme y=fonction_de_x et ça te trace les courbes.

[chadok]

Ta Casio, si elle est graphique, c'est juste du dépannage quand tu n'est pas devant ton PC !
Et si elle n'est pas graphique, personnellement, je trouve ce traceur de courbes parfait :
https://www.desmos.com/calculator

[iris75]

Pour la 1) j’ai trouver que ces courbes semblent avoir une même tangente T en A (1;3) c’est cela ?

[pascal16]

maintenant, vérification
(1;3) fait bien partie des deux courbes
dérivées
équations des tangentes pour x=1 pour les courbes f et g.