(re)salut.
La première équation

se résous relativement bien : on l'écrit sous la forme
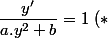)
, et il suffit de trouver une primitive

de la fonction

pour écrire (*) sous la forme
\!=\!1)
puis, en passant aux primitives,
\!=\!x\!+\!Cst)
et donc
\!=\!F^{-1}(x\!+\!Cst))
.
Et concernant la primitive F, si on veut rester dans R (et ne pas utiliser de complexes), ça va dépendre des signes de a et b : si les signes sont différent, on utilise une décomposition en éléments simple et on obtient une primitive "avec des log" et, si les signes sont les mêmes, on obtient une primitive avec de l'artangente. (je peut détailler ou te donner un lien pour plus de détail).
Concernant l'autre équation

, sur le principe théorique, c'est exactement la même chose :
on l'écrit

, c'est à dire
\!=\!1)
où

est une primitive de

et on conclue que
\!=\!F^{-1}(x\!+\!Cst))
.
Le "léger hic", c'est que les primitives de

, y'a peut-être éventuellement moyen de les trouver dans le cas particulier de l'exposant 1,4 , mais j'ai des doutes concernant le cas général d'un exposant quelconque.
Après, ça dépend aussi de la "forme" sous laquelle tu veut le résultat : si tu as des valeur numérique de a, de b et de y(0) et que tu veut des valeur numériques (avec une certaine précision) de y(t) pour certaines valeur de t (ou le graphe de la fonction y), il n'y a pas de problème : il y a des tonnes de logiciels qui font ce type de calculs.
D'un autre coté, si tu veut un résultat théorique et que tu accepte que ce résultat contienne ce qu'on appelle des
fonctions spéciales alors c'est peut-être jouable, mais avec que des "fonctions usuelles" (style log, arctan, etc...), j'ai des doutes (mais je suis pas sûr)
