Question th(a) Tangente hyperbolique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sigmal
- Messages: 4
- Enregistré le: 26 Avr 2018, 08:42
-
par sigmal » 26 Avr 2018, 08:58
Bonjour a tous,
dans le cadre de ma reprise d'etude, j'ai repris les maths.
Jai un DM a faire (non je ne vais pas demander la solution toute cuite), dans lequel on doit demontrer plusieurs choses :
-
 = 4ch^3(a) - 3ch(a))
,
-
 = 4sh^3(a) + 3sh(a))
-
 = \frac{th^3(a) + 3th(a)}{1 + 3th^2(a)})
Pour les deux premiers, pas de problème pour démontrer, je passe par les l'expression de ch/sh en expo et tout se passe bien. En revanche pour th(3a), impossible d'arriver a quelque chose de concret.
Est ce que quelqu'un aurait une piste pour la dernière demo, car je fais choux blanc.
Bonne journee a tous.
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
par Kolis » 26 Avr 2018, 09:03
Tu écris le quotient "sinh/cosh" et tu mets
)
en facteur au nuérateur et dénominateur.
-
sigmal
- Messages: 4
- Enregistré le: 26 Avr 2018, 08:42
-
par sigmal » 26 Avr 2018, 09:14
Salut,
merci pour la rep. mais je ne comprends pas bien,
j'ai tenté, sachant que les deux expressions du dessus sont demontrées de faire cela :
 = \frac{sh(3a)}{ch(3a)} = \frac{4sh^3(a) + 3sh(a)}{4ch^3(a) - 3ch(a)} = \frac{sh(a)}{ch(a)} *\frac{4sh^2(a) + 3}{4ch^2(a) - 3})
mais ca ne m'amene guere plus loin..
Modifié en dernier par
sigmal le 26 Avr 2018, 09:18, modifié 2 fois.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
par Pseuda » 26 Avr 2018, 09:17
Bonjour,
th(3a)=sh(3a)/ch(3a). Division en haut et en bas par ch^3(a).
Au dénominateur : utiliser la formule : ch^2(a)=1/(1-th^2(a)).
En haut, mettre sh(a) en facteur, et réutiliser la formule précédente.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 26 Avr 2018, 10:35
Bonjour,
autre piste
=th(2a+a)=\dfrac{th(2a)+th(a)}{1+th(2a)th(a)})
=\dfrac{2th(a)}{1+th^2(a)})
en remplaçant dans
....)
-
aviateur
par aviateur » 26 Avr 2018, 14:58
Bonjour
Encore une autre piste :
= i tan(a))
Cela pour dire que si on est à l'aise avec les fonctions trigonométriques on s'en sort de façon analogue
avec les fonctions hyperboliques (et inversement)
-
sigmal
- Messages: 4
- Enregistré le: 26 Avr 2018, 08:42
-
par sigmal » 27 Avr 2018, 08:11
Bonjour,
Merci a tous pour vos pistes. Cependant, je ne pense pas qu'il faille partir sur des formules deja toutes pretes, mais plutot se baser sur ce qui a été démontré auparavant (sh(3a) et ch(3a), plus haut)... Cependant je n'y arrive décidément pas haha.
merci pour votre aide dans tous les cas !
bonne journée
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
par Kolis » 27 Avr 2018, 17:08
Si tu considères que
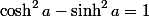
(ou encore :
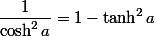
) comme "formule toute prête" et refuses de l'utiliser, je te souhaite bien du courage.
-
sigmal
- Messages: 4
- Enregistré le: 26 Avr 2018, 08:42
-
par sigmal » 27 Avr 2018, 18:08
Re,
Effectivement, il fallait partir de cette formule pour le denominateur et de
} = \frac{1}{th^2(a)} - 1)
en factorisant par
}{ch^3(a)})
et en remplacant dans l'expression le
})
et pareil pour le cosh ca fonctionne parfaitement.
Merci pour votre aide et bonne soiree (:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
