Exo d'algebre général
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jeremy58
- Membre Naturel
- Messages: 87
- Enregistré le: 01 Nov 2006, 14:45
-
par jeremy58 » 02 Nov 2006, 15:06
Vedeus a écrit:Un groupe fini
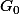
étant fixé, n'y aurait-il pas un nombre fini de morphismes
?
Ceci étant dit, si
désigne un automorphisme de
, alors on peut construire un morphisme
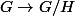
dont le noyau est
)
...
Je suis désolé mais je ne comprends pas tres bien vos indications.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 02 Nov 2006, 15:43
Je reprends la question de jeremy58 qui aurait mérité un deuxième fil car ici les questions et les réponses se croisent.
Le fait que G ait un nombre fini de générateurs entraîne que Aut(G) est fini car un automorphisme de G est déterminé par les images des générateurs.
On pose
=\{s_1,...,s_n\})
les sous groupes
)
sont distingués dans G et leur intersection K devrait réaliser ce qu'on veut.
-
Vedeus
- Membre Naturel
- Messages: 39
- Enregistré le: 13 Juin 2006, 14:27
-
par Vedeus » 02 Nov 2006, 15:53
jeremy58 a écrit:Je suis désolé mais je ne comprends pas tres bien vos indications.
Alors une nouvelle indication :
le sous-groupe
}{\bigcap}\varphi(H))
n'est-il pas un sous-groupe caractéristique de
?
-
Vedeus
- Membre Naturel
- Messages: 39
- Enregistré le: 13 Juin 2006, 14:27
-
par Vedeus » 02 Nov 2006, 15:55
yos a écrit:Le fait que G ait un nombre fini de générateurs entraîne que Aut(G) est fini
Non. Essaye
muni de l'addition.
Il y a une infinité d'automorphismes de ce groupe.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 02 Nov 2006, 17:01
Vedeus a écrit:Non. Essaye
muni de l'addition.
Il y a une infinité d'automorphismes de ce groupe.
Ah oui j'ai parlé trop vite. Mais ce que tu proposes plus haut est la même chose que moi : si on n'a pas la finitude de Aut(G), le fait que cette intersection soit d'indice finie est moins clair. Et même le fait qu'elle est non triviale.
-
Vedeus
- Membre Naturel
- Messages: 39
- Enregistré le: 13 Juin 2006, 14:27
-
par Vedeus » 02 Nov 2006, 18:31
yos a écrit:Ah oui j'ai parlé trop vite. Mais ce que tu proposes plus haut est la même chose que moi.
Non, relis bien ce que j'ai écris.
Je ne passe pas par la finitude de
)
mais par celle de l'ensemble
\;\mid \; \varphi \in Aut(G)\bigr\})
ce qui est moins fort mais suffisant.
-
jeremy58
- Membre Naturel
- Messages: 87
- Enregistré le: 01 Nov 2006, 14:45
-
par jeremy58 » 03 Nov 2006, 12:15
Je me pose une petite question qui n'a peut-etre aucun sens.
J'aurais voulu savois si vous pensiez que cet exo est toujours vrai si H n'est pas distingué?
-
Vedeus
- Membre Naturel
- Messages: 39
- Enregistré le: 13 Juin 2006, 14:27
-
par Vedeus » 03 Nov 2006, 14:19
jeremy58 a écrit:Je me pose une petite question qui n'a peut-etre aucun sens.
J'aurais voulu savois si vous pensiez que cet exo est toujours vrai si H n'est pas distingué?
Oui, parce que de toutes manières tu peux remplacer
par un sous-groupe distingué de
qui est inclus dans
et d'indice fini dans
(cf. premier exo du fil).
-
jeremy58
- Membre Naturel
- Messages: 87
- Enregistré le: 01 Nov 2006, 14:45
-
par jeremy58 » 04 Nov 2006, 14:37
Je ne comprends pas bien comment ker p peut-etre égal à phi(H)? ou p designe le morphisme de G dans G/H.
-
Vedeus
- Membre Naturel
- Messages: 39
- Enregistré le: 13 Juin 2006, 14:27
-
par Vedeus » 04 Nov 2006, 17:57
jeremy58 a écrit:Je ne comprends pas bien comment ker p peut-etre égal à phi(H)? ou p designe le morphisme de G dans G/H.
Il n'y a pas qu'un morphisme de
sur
.
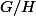
Si
est un automorphisme de
, il induit
un isomorphisme de
)
,
et alors en notant
} : \; G \rightarrow G/\varphi(H))
la projection canonique, le morphisme
^{-1} \circ \pi_{\varphi(H)} : \; G \rightarrow G/H)
a bien pour noyau
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
