Tu as presque fini , c'est pas le moment de craquer :hein: I est le milieu de [BC] et comme BECD est un parallélogramme c'est aussi ...
Imod
Géometrie dans l'espace
42 messages
- Page 2 sur 3 - 1, 2, 3
par Krys933 » 28 Oct 2006, 14:38
j'ai répondu la chose suivante:
Puisque E est le symetrique de A par rapport à B le vecteur BE est colinéaire au vecteur DC ; le quadrilatere DCBE est donc un parallélogramme (un parallélogramme est un quadrilatère dont les coté sont parallèles deux à deux). De plus on sait que les diagonales d'un parallélogramme se coupe en leurs milieux, donc I est le milieu de [DE] on a donc:
vect DI = 1/2 vect DE
D I E sont donc alignées....
Ca vous parait correct, pas d'erreur de formulation ou meme de raisonnement?
Vous auriez une solution à la question 2) ?
Merci d'avance
Puisque E est le symetrique de A par rapport à B le vecteur BE est colinéaire au vecteur DC ; le quadrilatere DCBE est donc un parallélogramme (un parallélogramme est un quadrilatère dont les coté sont parallèles deux à deux). De plus on sait que les diagonales d'un parallélogramme se coupe en leurs milieux, donc I est le milieu de [DE] on a donc:
vect DI = 1/2 vect DE
D I E sont donc alignées....
Ca vous parait correct, pas d'erreur de formulation ou meme de raisonnement?
Vous auriez une solution à la question 2) ?
Merci d'avance
par Imod » 28 Oct 2006, 15:04
Avant d'attaquer la question 2 , il faut mettre un peu d'ordre dans la première .
1°) Une façon extrêmement rapide et efficace de montrer qu'un quadrilatère BECD est un parallélogramme est de montrer que les vecteurs BE et DC sont égaux ( et la réciproque est vraie ) .
Quand tu dis "Puisque E est le symétrique de A par rapport à B le vecteur BE est colinéaire au vecteur DC " on ne suit pas ta logique . Dis plutôt : E est le symétrique de A par rapport à B alors les vecteurs AB et BE sont égaux et comme les vecteurs AB et DC sont aussi égaux pour une raison que je te laisse trouver , alors les vecteurs BE et DC sont égaux .
2°) Pour montrer que D,I et E sont alignés , il suffit de montrer que I est le milieu de [DE] . La encore il faut partir des données I est le milieu de [BC] et comme BECD ...
Imod
1°) Une façon extrêmement rapide et efficace de montrer qu'un quadrilatère BECD est un parallélogramme est de montrer que les vecteurs BE et DC sont égaux ( et la réciproque est vraie ) .
Quand tu dis "Puisque E est le symétrique de A par rapport à B le vecteur BE est colinéaire au vecteur DC " on ne suit pas ta logique . Dis plutôt : E est le symétrique de A par rapport à B alors les vecteurs AB et BE sont égaux et comme les vecteurs AB et DC sont aussi égaux pour une raison que je te laisse trouver , alors les vecteurs BE et DC sont égaux .
2°) Pour montrer que D,I et E sont alignés , il suffit de montrer que I est le milieu de [DE] . La encore il faut partir des données I est le milieu de [BC] et comme BECD ...
Imod
par Krys933 » 28 Oct 2006, 15:19
BECD est un parallélogramme. On sait donc que I est le milieu de [DE] car ds un para les diagonales se coupent en leurs milieu ....
par Imod » 28 Oct 2006, 15:27
Pour la deuxième question tu as déjà eu pas mal d'indications , j'en ajoute une autre , comment appelerais-tu les droites (EJ) et (SB) dans le triangle SAE ?
Imod
Imod
par Krys933 » 28 Oct 2006, 16:12
BA MERCI beaucoup j'ai fini enfin l'exo 2 je vois pas trop comment ca se traduit mathématiquement je suis d'accord mai mathématiquement ...
par Imod » 28 Oct 2006, 16:22
C'est une propriété connue le centre de gravité d'un triangle se situe aux 2/3 des médianes en partant des sommets .
Imod
Imod
par Krys933 » 28 Oct 2006, 16:31
Critiquer le raisonnement suivant; " vecteur AB et vecteur CD sont des vacteurs coplanaires , donc les pt A B C D sont coplanaires "
je te parle de ceci lol
je te parle de ceci lol
par Imod » 28 Oct 2006, 16:53
Une réponse de Quidam :
Le problème est que l'on peut pas parler de vecteurs coplanaires qu'est-ce que cela pourrait vouloir dire ?
1°) u et v sont coplanaires s'il existe u=AB et v=CD avec A,B,C,D coplanaires mais alors tous les paires de vecteurs sont coplanaires et comme il existent des quadruplets de points non coplanaires la propriété est fausse .
2°) u et v sont coplanaires si pour tout u=AB et v=CD alors A,B,C,D sont coplanaires mais alors u et v sont colinéaires et la notion n'a pas grand intérêt mais la propriété est vraie .
Il est vrai que l'argumentation n'est pas facile . Je te laisse faire le tri .
Imod
Quidam a écrit:Moi je trouve ça tout à fait faux !
Si les quatre murs de ma chambre font respectivement face au Nord, à l'Ouest, au Sud et à l'Est, un vecteur colinéaire à l'intersection de mon mur Nord et du sol, est coplanaire à un vecteur colinéaire à l'intersection du mur Sud et du mur Est. Pourtant, les quatre points extrémités respectives de ces deux segments ne sont pas coplanaires !
Le problème est que l'on peut pas parler de vecteurs coplanaires qu'est-ce que cela pourrait vouloir dire ?
1°) u et v sont coplanaires s'il existe u=AB et v=CD avec A,B,C,D coplanaires mais alors tous les paires de vecteurs sont coplanaires et comme il existent des quadruplets de points non coplanaires la propriété est fausse .
2°) u et v sont coplanaires si pour tout u=AB et v=CD alors A,B,C,D sont coplanaires mais alors u et v sont colinéaires et la notion n'a pas grand intérêt mais la propriété est vraie .
Il est vrai que l'argumentation n'est pas facile . Je te laisse faire le tri .
Imod
par Krys933 » 28 Oct 2006, 17:12
tu veux que mon cerveau lache prise c ca? je reconnais en toi une personne tres forte mais qui veux me degouter lol , pourrais tu me donner la solution parce que bon entre parenthese j'ai d'autre DM de math (oui j'ai deux prof de math c bizarre :S) et l'autre DM m'a lair bien pire !!!!!
par Imod » 28 Oct 2006, 17:37
Krys933 a écrit:tu veux que mon cerveau lache prise c ca? je reconnais en toi une personne tres forte mais qui veux me degouter lol , pourrais tu me donner la solution parce que bon entre parenthese j'ai d'autre DM de math (oui j'ai deux prof de math c bizarre :S) et l'autre DM m'a lair bien pire !!!!!
Je ne me fiche absolument pas de toi , je t'ai dit ce que je sais et je ne vois pas quoi dire d'autre . Il est vrai que pour moi le lycée date d'il y a très longtemps et je ne vois pas d'arguments clair pour expliquer pourquoi c'est faux , mais quelqu'un d'autre aura peut-être une idée ?
Imod
par Krys933 » 28 Oct 2006, 17:38
hum ok , ba je lance un avis national ..... :help: :help: :help: :help:
par Quidam » 28 Oct 2006, 18:14
Krys933 a écrit:-Critiquer le raisonnement suivant; " vecteur AB et vecteur CD sont des vacteurs coplanaires , donc les pt A B C D sont coplanaires "
Je ne vois pas où est le problème ! Comme le dit Imod, on ne parle pas en général de vecteurs coplanaires. Cependant, on peut facilement donner un sens à cette expression. On peut dire que deux vecteurs sont coplanaires s'il existe un plan où l'on pourrait loger deux de leurs représentants respectifs. Mais dans ce cas tous les couples de deux vecteurs sont coplanaires ! On n'a qu'à choisir un plan qui serait perpendiculaire à un vecteur lui-même perpendiculaire à chacun des deux vecteurs donnés. Et pourtant tous les quadruplets de points ne sont pas coplanaires. Dans l'exemple ci-contre d'un parallélépipède rectangle, analogue à l'exemple "expliqué" dans un post précédent, les vecteurs
par Imod » 29 Oct 2006, 02:44
Krys933 a écrit:Critiquer le raisonnement suivant; " vecteur AB et vecteur CD sont des vecteurs coplanaires , donc les pt A B C D sont coplanaires "
Je reviens une dernière fois sur cette phrase qui me pose vraiment problème , je ne veux pas embêter Kryss933 , je m'adresse plutôt à Quidam ou à d'autres personnes qui ont suivi le fil , après j'arrête car ça vire à l'obsession :mur:
Le problème est bien dans la définition de deux vecteurs coplanaires , il y a deux façons de voir les choses , celle de Quidam qui revient à dire que tous les vecteurs sont coplanaires et la mienne qui revient à dire que deux vecteurs sont coplanaires s'ils sont colinéaires . Nous sommes bien d'accord que ces deux définitions sont sans intérêt mais , gros dilemme , avec la définition de Quidam le raisonnement proposé est faux , avec la mienne il est juste . Je ne pense pas cette analyse soit celle qu'attend le professeur qui a donné le sujet donc la question est mal posée .
Personnellement j'aurais plutôt proposé à la critique : "on dit que deux vecteurs u et v sont coplanaires s'il existe quatre points A,B,C,D coplanaires tels que u=AB et v=CD" . La réponse attendue étant que tous les vecteurs sont coplanaires donc la définition est sans intérêt .
Bon je laisse tomber pour ce soir et bonne nuit à ceux qui ne dorment pas encore .
Imod
par Quidam » 29 Oct 2006, 14:37
Imod, je suis bien surpris de ton dernier post. J'avais cru (28/10-00.36) que tu étais d'accord avec moi car ton apparent désaccord n'aurait été dû qu'à une faute d'inattention !
Il est vrai que le terme "coplanaire" m'a dérouté, puisqu'il s'agit de vecteurs. Mais j'ai immédiatement trouvé une acception qui m'a semblé la seule possible : "deux vecteurs sont coplanaires s'il existe un plan contenant un représentant de chacun d'eux. Le fait que deux vecteurs soient toujours coplanaires explique d'abord que cet emploi du vocable soit si rare. Mais cela ne me gêne pas. Il me semble que le but de l'exercice est de faire prendre conscience aux élèves que le fait que si deux vecteurs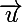
et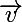 
peuvent se placer dans un même plan cela n'implique pas que
[
et  \Rightarrow (A,B,C,D))
sont coplanaires].
Lorsque tu dis :
je ne peux pas être d'accord avec la deuxième possibilité de définition. A mon sens il est impossible de donner cette interprétation au terme "coplanaire", car pourquoi alors ne pas utiliser le mot "colinéaire" ?
Enfin, lorsque tu écris :
ta conclusion "Je ne pense pas cette analyse soit celle qu'attend le professeur", j'avoue que je trouve cette phrase ambiguë car je ne parviens pas à déterminer à quelle définition se rapporte le mot "cette" : le mot "cette" désigne-t-il la définition que j'ai prise, ou la tienne ?
Mais, coup de théâtre, voilà que tu te rallies à ma définition :
Je ne peux que me joindre à cette conclusion, puisque finalement, tu es bien d'accord avec moi. Je ne crois pas que la question soit mal posée. Pour compléter ma perception de l'intention du professeur, je dirais que le but est de faire désapprendre aux élèves que deux droites sont soit parallèles soit concourantes : c'est vrai dans le plan, cela ne l'est pas dans l'espace ! Et si les élèves perçoivent que deux vecteurs sont toujours coplanaires et que par conséquent, certes la définition est sans intérêt, mais surtout le fait que deux vecteurs soient coplanaires ne prouve absolument rien puisque c'est toujours le cas, alors le professeur a réussi ce qu'il voulait faire !
Il est vrai que le terme "coplanaire" m'a dérouté, puisqu'il s'agit de vecteurs. Mais j'ai immédiatement trouvé une acception qui m'a semblé la seule possible : "deux vecteurs sont coplanaires s'il existe un plan contenant un représentant de chacun d'eux. Le fait que deux vecteurs soient toujours coplanaires explique d'abord que cet emploi du vocable soit si rare. Mais cela ne me gêne pas. Il me semble que le but de l'exercice est de faire prendre conscience aux élèves que le fait que si deux vecteurs
[
Lorsque tu dis :
Imod a écrit:Le problème est que l'on peut pas parler de vecteurs coplanaires qu'est-ce que cela pourrait vouloir dire ?
1°) u et v sont coplanaires s'il existe u=AB et v=CD avec A,B,C,D coplanaires mais alors tous les paires de vecteurs sont coplanaires et comme il existent des quadruplets de points non coplanaires la propriété est fausse .
2°) u et v sont coplanaires si pour tout u=AB et v=CD alors A,B,C,D sont coplanaires mais alors u et v sont colinéaires et la notion n'a pas grand intérêt mais la propriété est vraie .
je ne peux pas être d'accord avec la deuxième possibilité de définition. A mon sens il est impossible de donner cette interprétation au terme "coplanaire", car pourquoi alors ne pas utiliser le mot "colinéaire" ?
Enfin, lorsque tu écris :
Imod a écrit:il y a deux façons de voir les choses , celle de Quidam qui revient à dire que tous les vecteurs sont coplanaires et la mienne qui revient à dire que deux vecteurs sont coplanaires s'ils sont colinéaires . Nous sommes bien d'accord que ces deux définitions sont sans intérêt mais , gros dilemme , avec la définition de Quidam le raisonnement proposé est faux , avec la mienne il est juste . Je ne pense pas cette analyse soit celle qu'attend le professeur qui a donné le sujet donc la question est mal posée .
ta conclusion "Je ne pense pas cette analyse soit celle qu'attend le professeur", j'avoue que je trouve cette phrase ambiguë car je ne parviens pas à déterminer à quelle définition se rapporte le mot "cette" : le mot "cette" désigne-t-il la définition que j'ai prise, ou la tienne ?
Mais, coup de théâtre, voilà que tu te rallies à ma définition :
Imod a écrit:Personnellement j'aurais plutôt proposé à la critique : "on dit que deux vecteurs u et v sont coplanaires s'il existe quatre points A,B,C,D coplanaires tels que u=AB et v=CD" . La réponse attendue étant que tous les vecteurs sont coplanaires donc la définition est sans intérêt .
Je ne peux que me joindre à cette conclusion, puisque finalement, tu es bien d'accord avec moi. Je ne crois pas que la question soit mal posée. Pour compléter ma perception de l'intention du professeur, je dirais que le but est de faire désapprendre aux élèves que deux droites sont soit parallèles soit concourantes : c'est vrai dans le plan, cela ne l'est pas dans l'espace ! Et si les élèves perçoivent que deux vecteurs sont toujours coplanaires et que par conséquent, certes la définition est sans intérêt, mais surtout le fait que deux vecteurs soient coplanaires ne prouve absolument rien puisque c'est toujours le cas, alors le professeur a réussi ce qu'il voulait faire !
par Imod » 29 Oct 2006, 15:13
Quidam ,
je suis entièrement d'accord avec toi sur l'objectif du professeur qui est sans aucun doute d'inciter l'élève à produire un développement comme le tien . Là où je suis moins d'accord c'est quand tu dis que la seule définition raisonnable de deux vecteurs coplanaires est : deux vecteurs sont coplanaires s'ils admettent deux représentants coplanaires . La définition qui dirait : deux vecteurs sont coplanaires si tout représentant de l'un est coplanaire avec tout représentant de l'autre , n'est pas ridicule . L'argument disant cette définition n'est pas intéressante car elle définit deux vecteurs colinéaires peut s'appliquer de même à la première définition qui définit deux vecteurs coplanaires comme deux vecteurs quelconques . Si on admet que ces deux définitions ( peu glorieuses ) ont un sens , l'élément de démonstration que le professeur propose à la critique est :
- faux avec ta définition et on peut argumenter comme tu l'as fait .
- vrai avec ma définition car si les vecteurs AB et CD sont coplanaires alors les représentant AB et CD sont coplanaires .
C'est uniquement pour cette raison que je proposais une autre formulation de la question qui enfermerait l'élève dans "ta" définition pour l'obliger à argumenter comme tu l'as fait .
Imod
je suis entièrement d'accord avec toi sur l'objectif du professeur qui est sans aucun doute d'inciter l'élève à produire un développement comme le tien . Là où je suis moins d'accord c'est quand tu dis que la seule définition raisonnable de deux vecteurs coplanaires est : deux vecteurs sont coplanaires s'ils admettent deux représentants coplanaires . La définition qui dirait : deux vecteurs sont coplanaires si tout représentant de l'un est coplanaire avec tout représentant de l'autre , n'est pas ridicule . L'argument disant cette définition n'est pas intéressante car elle définit deux vecteurs colinéaires peut s'appliquer de même à la première définition qui définit deux vecteurs coplanaires comme deux vecteurs quelconques . Si on admet que ces deux définitions ( peu glorieuses ) ont un sens , l'élément de démonstration que le professeur propose à la critique est :
- faux avec ta définition et on peut argumenter comme tu l'as fait .
- vrai avec ma définition car si les vecteurs AB et CD sont coplanaires alors les représentant AB et CD sont coplanaires .
C'est uniquement pour cette raison que je proposais une autre formulation de la question qui enfermerait l'élève dans "ta" définition pour l'obliger à argumenter comme tu l'as fait .
Imod
par Quidam » 29 Oct 2006, 16:25
Je pense bien avoir compris ce que tu dis, mais cela ne me convainc pas ! Je ne vois vraiment pas l'intérêt de définir deux vecteurs coplanaires comme "deux vecteurs colinéaires" !
J'aimerais bien que des experts interviennent !
Par ailleurs, je compatis au désespoir de Krys233, qui aimerait sûrement bien voir émerger un consensus...Désolé Krys ! On fait ce qu'on peut ! Il faudra bien que tu choisisses une réponse !
Quoi qu'il en soit, ce sera sympa de ta part de nous faire savoir "après la correction" ce que voulait ton professeur dans cette question !
J'aimerais bien que des experts interviennent !
Par ailleurs, je compatis au désespoir de Krys233, qui aimerait sûrement bien voir émerger un consensus...Désolé Krys ! On fait ce qu'on peut ! Il faudra bien que tu choisisses une réponse !
Quoi qu'il en soit, ce sera sympa de ta part de nous faire savoir "après la correction" ce que voulait ton professeur dans cette question !
par Imod » 29 Oct 2006, 18:42
Quidam a écrit:J'aimerais bien que des experts interviennent !
Je ne parle pas en tant qu'expert mais je me suis renseigné : deux vecteurs sont coplanaires s'ils sont dans un même plan ( vectoriel ) ce qui est toujours vrai car la dimension de l'espace engendré par les deux vecteurs est inférieure ou égale à 2 . Donc la bonne définition est celle de Quidam et le raisonnement à critiquer est faux car la première partie de la phrase "les vecteurs AB et CD sont coplanaires" est toujours vraie et la deuxième "A , B , C ,D sont coplanaires" pas toujours .
Pour moi le problème est ( enfin ) clos :zen: , je maintiens que cet exercice est difficile car il utilise implicitement une notion : "vecteurs coplanaires" qui n'est pas connue des élèves mais je ne vais pas rouvrir le débat :marteau: .
En tout cas bon courage à Kryss933 pour la suite de son devoir et merci beaucoup à Quidam pour sa patience :we:
Imod
42 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :