Série numérique à terme général complexe

par **marawita1** » 06 Aoû 2016, 13:02

Bonjour,

Je veux savoir la convergence de la série numérique dont le terme général est

suivant les réels

et

.

Un cas particulier: si

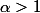
, il est clair que la série converge absolument et par suite converge pour tout

.

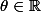
Merci d'avance.

par **Kolis** » 06 Aoû 2016, 13:15

Bonjour !
Si

aussi tu as un résultat immédiat.

On peut, si tu le connais, utiliser le théorème d'Abel...

Si tu ne connais pas ce théorème, soit

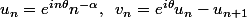
. Calcules

et montres que

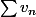
est une série absolument convergente. Ensuite, trouves une relation entre les sommes partielles d'ordre

pour les séries

...

par **zygomatique** » 06 Aoû 2016, 13:30

salut

un autre cas particulier :

t est multiple (entier) de pi et a > 0 (série alternée)

...

par **Razes** » 06 Aoû 2016, 15:04

par **marawita1** » 06 Aoû 2016, 21:41

Merci pour vos réponses.

Juste le cas où

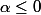
, je sais pas comment le faire!!!!!!!

par **Razes** » 07 Aoû 2016, 03:26

Nous avons

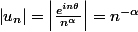
, donc

ne tends pas vers zéro donc la série diverge.

par **marawita1** » 07 Aoû 2016, 11:30

Merci bien.