Suite

[biss]

avec n≥1
1) montrer que Un est strictement croissante. C'est fait
2) montrer que (1)
Comment j'ai fais ?
Du (1) j'en ai coulé que (2)
Puis j'ai dis que démontrer (1) revient à démontrer (2) et j'ai démontrer que (2) est vrai donc (1) est vrai. Est je juste ou comment vous voyez ?

[Sake]

avec n≥1
1) montrer que Un est strictement croissante. C'est fait
2) montrer que (1)
Comment je fais ?

Par récurrence, par exemple.

[paquito]

Bonjour,

Le 1) est évident
le 2) se fait bien par récurrence.
Après, je ne comprend rien à ton charabia! peux tu expliquer ce que tu veux obtenir S.V.P.

[biss]

Je n'arrive pas à le faire par récurrence.
Je voulais dire que en me servant de (1), je tire (2) puis je fais la récurrence en (2) pour montrer (1)

[biss]

A moins que j'atoute a chaque côté de l'égalité.

[zygomatique]

salut












Edit : bon j'ai m... dans les valeurs de la suite ... mais le principe est là et on peut se passer de la récurrence ....

[biss]

Je te remerci Zygomatique. Mais est ce que j'ai dis a la 1er poste est acceptable ?

[biss]

Pour me faire plus comprendre j'ai fais.
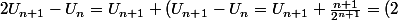le (2) est précisé plus haut.
Puis je démontre le (2) par reccurence et j'en conclu que le (1) est vrai.

[zygomatique]

démontrer que ::

(1) <=> (2)
(2)

convient effectivement ...

[aymanemaysae]

Le que vous avez trouvé dans votre premier post diffère de celui que j'ai trouvé : .

Pour le plaisir, et malgré que c'est saugrenue comme démarche, je l'édite pour partager avec vous une autre façon de faire:

Pour x ]0,1[,





Donc pour on a , ce qui donne .

[biss]

Le que vous avez trouvé dans votre premier post diffère de celui que j'ai trouvé : .

Pour le plaisir, et malgré que c'est saugrenue comme démarche, je l'édite pour partager avec vous une autre façon de faire:

Pour x ]0,1[,





Donc pour on a , ce qui donne .

Pourtant c'était ma premiere idée, le était ma première idée, seulement je ne savais pas comment continué, merci.