Exercice inventé
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 14 Déc 2015, 14:06
par Pierrot73 » 14 Déc 2015, 14:06
Lovile a écrit:Donc [BB'] =1/2-x ?
Almost ; [BB'] = 1-x (ce qui est bien la moitié de 2-2x).
Maintenant, fais pareil en projetant B sur une droite verticale (que je te laisse déterminer). En choisissant la bonne droite, tu auras un triangle rectangle dont un des côtés sera le rayon de C2 et tu pourras déterminer x.
-
Lovile
- Membre Naturel
- Messages: 12
- Enregistré le: 14 Déc 2015, 10:22
-
 par Lovile » 14 Déc 2015, 15:59
par Lovile » 14 Déc 2015, 15:59
Pierrot73 a écrit:Almost ; [BB'] = 1-x (ce qui est bien la moitié de 2-2x).
Maintenant, fais pareil en projetant B sur une droite verticale (que je te laisse déterminer). En choisissant la bonne droite, tu auras un triangle rectangle dont un des côtés sera le rayon de C2 et tu pourras déterminer x.
Je pense que je peux projeter B sur la droite verticale au point O et ainsi je tombe sur un segment [BK]=1/2*x

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 14 Déc 2015, 16:07
par Pierrot73 » 14 Déc 2015, 16:07
Lovile a écrit:Je pense que je peux projeter B sur la droite verticale au point O et ainsi je tombe sur un segment [BK]=1/2*x
Ok, mais dans ce cas, ton triangle (B, B', B''), avec B'' le projeté orthogonal de B sur la droite verticale, ne tire nullement partie du fait que C2 a un rayon de 1. Il faut qu'un des côtés du triangle soit le rayon de C2.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 14 Déc 2015, 16:21
par zygomatique » 14 Déc 2015, 16:21
salut
avec la trigonométrie (cachée plus ou moins derrière une solution donnée au dessus)
a : réel repérant le point A dans le cercle trigonométrique C1
les coordonnées de A sont (cos a; sin a)
alors ::
x/2 = 1 - cos a cos a = 1 - x/2
x = 1 + sin a sin a = x - 1
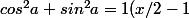^2 + (x - 1)^2 = 1)
....
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 14 Déc 2015, 16:31
par Pierrot73 » 14 Déc 2015, 16:31
zygomatique a écrit:salut
avec la trigonométrie (cachée plus ou moins derrière une solution donnée au dessus)
a : réel repérant le point A dans le cercle trigonométrique C1
les coordonnées de A sont (cos a; sin a)
alors ::
x/2 = 1 - cos a cos a = 1 - x/2
x = 1 + sin a sin a = x - 1
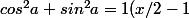^2 + (x - 1)^2 = 1)
....
:lol3:
Et on retombe sur l'équation de C2 ou sur ce vers quoi va tendre Lovile avec les projections orthogonales ! La boucle est bouclée zygomatique :we: :we: (je dirais même à cette occasion que le cercle trigo est bouclé !)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 14 Déc 2015, 16:37
par chan79 » 14 Déc 2015, 16:37

Pour compléter:
une construction classique de ce petit carré.
On place le milieu O de [CD].
On obtient G et H en traçant les droites (OE) et (OF).
On mène les perpendiculaires à (CD) pour avoir I et J.
On vérifie que GHIJ est bien un carré.
On peut remarquer que D, G et B sont alignés (on peut retrouver le coté du petit carré avec Thalès).

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 14 Déc 2015, 17:43
par zygomatique » 14 Déc 2015, 17:43
On peut remarquer que D, G et B sont alignés (on peut retrouver le coté du petit carré avec Thalès).
c'est d'ailleurs une autre possibilité de construction :: (avec tes notations)
je place un point G sur C1 quelconque (mais dans le bon quadrant bien sur) et je construis le carré GJIH avec J sur (la droite (CD) ...
bien sur I sera aussi sur (CD) mais H lui sera "quelconque" ...
alors en considérant l'homothétie de centre D "convenable" (ie de bon rapport k à déterminer) on construit le bon carré ...
indice : considérer le point d'intersection des droites (DG) et (BC) puis Thalès ...
un classique de seconde pour inscrire un carré dans un triangle du temps où on voyait les homothétie "sérieusement" en seconde ....
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Lovile
- Membre Naturel
- Messages: 12
- Enregistré le: 14 Déc 2015, 10:22
-
 par Lovile » 14 Déc 2015, 18:24
par Lovile » 14 Déc 2015, 18:24
J'ai compris la méthode de chan 79 mais j'ai du mal avec sinus et cosinus de a, vous pouvez me ré expliquer s'il vous plaît ? Après promis je ne vous embête plus !!

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 15 Déc 2015, 08:07
par Pierrot73 » 15 Déc 2015, 08:07
Lovile a écrit:J'ai compris la méthode de chan 79 mais j'ai du mal avec sinus et cosinus de a, vous pouvez me ré expliquer s'il vous plaît ? Après promis je ne vous embête plus !!
Bonjour Lovile,
A appartient au cercle C1 de rayon 1, comme le cercle trigonométrique.
Donc, tu peux construire un triangle rectangle dont l'hypoténuse est le rayon du cercle, et les deux petits cotés le cosinus et le sinus de A. Tu sais que cos²(A) + sin²(A) = 1.
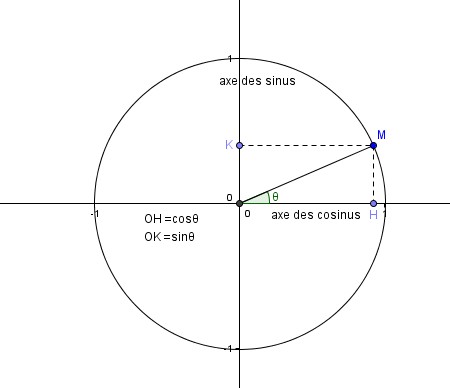
Reste la question de comment exprimer cos(A) ou sin(A) en fonction de x. Comme l'a écrit zygomatique cos(A) = 1 - x/2 et sin(A) = x - 1.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Déc 2015, 14:43
par chan79 » 15 Déc 2015, 14:43
Au lieu du carré, on pourrait mettre un triangle équilatéral :zen:

-
Krokenoverir
- Membre Naturel
- Messages: 13
- Enregistré le: 20 Nov 2015, 19:25
-
 par Krokenoverir » 17 Déc 2015, 20:25
par Krokenoverir » 17 Déc 2015, 20:25
J'ai trouvé [HH']=1-x [HB]=1 [H'B]=(1-x)/2
mais après je fais quoi ?
Et je ne savais pas que cos²(A) + sin²(A) = 1.

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 18 Déc 2015, 09:22
par Pierrot73 » 18 Déc 2015, 09:22
Krokenoverir a écrit:J'ai trouvé [HH']=1-x [HB]=1 [H'B]=(1-x)/2
mais après je fais quoi ?
Et je ne savais pas que cos²(A) + sin²(A) = 1.
le triangle HBH' est rectangle, donc avec Pythagore, tu trouves x.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 18 Déc 2015, 10:09
par chan79 » 18 Déc 2015, 10:09
Pythagore dans le triangle bleu fait l'affaire

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 108 invités




