Exercice inventé
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Lovile
- Membre Naturel
- Messages: 12
- Enregistré le: 14 Déc 2015, 10:22
-
 par Lovile » 14 Déc 2015, 10:58
par Lovile » 14 Déc 2015, 10:58
Bonjour,
Notre professeur nous a donné un exercice qu'il a lui même inventé. Nous étudions rien ce moment les fonctions dérivées.

Dans cette figure nous devons trouver x soit un côté du carrée mais je ne trouve aucun moyen d'avancer. J'ai essayer de faire l'aire l'aire du rectangle moins l'aire du carrée x^2 mais sans résultat.
J'aurais besoins de votre aide.
Merci beaucoup !

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 14 Déc 2015, 11:24
par chan79 » 14 Déc 2015, 11:24
Simplement Pythagore.
A toi de trouver le bon triangle rectangle.

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 14 Déc 2015, 11:31
par Pierrot73 » 14 Déc 2015, 11:31
Bonjour,
Si tu as vu les équations de cercle, tu peux procéder de la manière suivante :
En considérant le carré de droite de ta figure, et en positionnant l'origine O du repère en bas à gauche du grand carré, ton cercle C2 est un cercle de centre (1, 1) et de rayon 1. Son équation est donc (x-1)²+(y-1)²=1.
Il faut déterminer le point B de C2 de coordonnées (x/2, x). Note que x doit être inférieur à 1.
-
Lovile
- Membre Naturel
- Messages: 12
- Enregistré le: 14 Déc 2015, 10:22
-
 par Lovile » 14 Déc 2015, 11:37
par Lovile » 14 Déc 2015, 11:37
chan79 a écrit:Simplement Pythagore.
A toi de trouver le bon triangle rectangle.
J'ai cherché Pythagore dans les carrés ou dans les quarts de cercle mais je n'ai rien trouvé...
-
Lovile
- Membre Naturel
- Messages: 12
- Enregistré le: 14 Déc 2015, 10:22
-
 par Lovile » 14 Déc 2015, 11:50
par Lovile » 14 Déc 2015, 11:50
Pour le point b je ne suis pas sur que y=x/2 et nous n'avons pas vu les équations de cercle

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 14 Déc 2015, 11:57
par Pierrot73 » 14 Déc 2015, 11:57
Lovile a écrit:Pour le point b je ne suis pas sur que y=x/2 et nous n'avons pas vu les équations de cercle
En ne considérant que le carré de droite et en plaçant l'origine du repère au sommet bas-gauche de ce carré, la coordonnée de B sur (Ox) vaut x/2, et celle sur (Oy) vaut x. Donc on a un point de coordonnées (x/2, x). Vu que ton cercle est de rayon 1 et qu'il est tangent à (Ox) et (Oy), tu peux déduire que son centre est de coordonnées (1, 1). Donc tu as bien l'équation de ton cercle (mais comme tu n'as pas vu les éq. de cercle, c'était juste pour préciser un peu).
La méthode de Chan79 marche très bien

Il faut (en tout cas c'est comme cela que j'ai fait) trouver un triangle dont l'un des côté soit le rayon du cercle, et exprimer les deux autres côtés en fonction de x.
-
Lovile
- Membre Naturel
- Messages: 12
- Enregistré le: 14 Déc 2015, 10:22
-
 par Lovile » 14 Déc 2015, 12:18
par Lovile » 14 Déc 2015, 12:18
Pierrot73 a écrit:En ne considérant que le carré de droite et en plaçant l'origine du repère au sommet bas-gauche de ce carré, la coordonnée de B sur (Ox) vaut x/2, et celle sur (Oy) vaut x. Donc on a un point de coordonnées (x/2, x). Vu que ton cercle est de rayon 1 et qu'il est tangent à (Ox) et (Oy), tu peux déduire que son centre est de coordonnées (1, 1). Donc tu as bien l'équation de ton cercle (mais comme tu n'as pas vu les éq. de cercle, c'était juste pour préciser un peu).
La méthode de Chan79 marche très bien

Il faut (en tout cas c'est comme cela que j'ai fait) trouver un triangle dont l'un des côté soit le rayon du cercle, et exprimer les deux autres côtés en fonction de x.
J'ai de suite pensé au triangle ayant rectangle ayant comme sommet le pont (1,1) mais je ne sais pas comment exprimer les deux côtés en fonction de x. Je pense notamment au côté d'en bas qui vaut 2x

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 14 Déc 2015, 12:21
par Pierrot73 » 14 Déc 2015, 12:21
Lovile a écrit:Je pense notamment au côté d'en bas qui vaut 2x
Que veux-tu dire ? S'agit-t-il du côté du carré que tu dois trouver ou bien du côté du rectangle "global" (auquel cas, il faut juste 2) ?
-
Lovile
- Membre Naturel
- Messages: 12
- Enregistré le: 14 Déc 2015, 10:22
-
 par Lovile » 14 Déc 2015, 12:29
par Lovile » 14 Déc 2015, 12:29
Pierrot73 a écrit:Que veux-tu dire ?
Si on note l'origine du repére 0 et le point V(1.0) et W(0,1) le triangle VON est un triangle rectangle équilatéral et VW=2x mais je ne sais pas comment l'expliquer.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 14 Déc 2015, 12:30
par chan79 » 14 Déc 2015, 12:30
Lovile a écrit:J'ai cherché Pythagore dans les carrés ou dans les quarts de cercle mais je n'ai rien trouvé...
Comme toujours, il ne faut pas hésiter à rajouter des éléments à la figure, comme des segments, des droites...

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 14 Déc 2015, 12:38
par Pierrot73 » 14 Déc 2015, 12:38
Lovile a écrit:Si on note l'origine du repére 0 et le point V(1.0) et W(0,1) le triangle VON est un triangle rectangle équilatéral et VW=2x mais je ne sais pas comment l'expliquer.
Je suis un peu perdu :we:
Où se trouve ton point O ? Où est ton point N ?
-
Lovile
- Membre Naturel
- Messages: 12
- Enregistré le: 14 Déc 2015, 10:22
-
 par Lovile » 14 Déc 2015, 12:54
par Lovile » 14 Déc 2015, 12:54
Pierrot73 a écrit:Je suis un peu perdu :we:
Où se trouve ton point O ? Où est ton point N ?
VOW pardon

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 14 Déc 2015, 13:02
par Pierrot73 » 14 Déc 2015, 13:02
Lovile a écrit:VOW pardon
OK. Donc, si on résume, tu as défini les points suivants : O (0, 0), V(1, 0) et W(0,1).
Le triangle VON est un triangle rectangle isocèle (et non équilatéral :lol3: ). Les côtés OV et OW sont donc égaux et valent combien ? Du coup, que vaut VW selon Pythagore ?
-
Lovile
- Membre Naturel
- Messages: 12
- Enregistré le: 14 Déc 2015, 10:22
-
 par Lovile » 14 Déc 2015, 13:10
par Lovile » 14 Déc 2015, 13:10
Pierrot73 a écrit:OK. Donc, si on résume, tu as défini les points suivants : O (0, 0), V(1, 0) et W(0,1).
Le triangle VON est un triangle rectangle isocèle (et non équilatéral :lol3: ). Les côtés OV et OW sont donc égaux et valent combien ? Du coup, que vaut VW selon Pythagore ?
OV et OW valent 1 mais je ne sais pas combien en les exprimant avec x

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 14 Déc 2015, 13:20
par Pierrot73 » 14 Déc 2015, 13:20
Lovile a écrit:OV et OW valent 1 mais je ne sais pas combien en les exprimant avec x
Oui, ils valent bien 1, donc VW vaut racine(2).
Malheureusement, ces infos ne vont pas beaucoup t'aider.
Essaie de partir sur cette piste :
Soit la droite (d) horizontale d'équation y = 1. Soit B' le projeté orthogonal de B sur (d) ? Exprime la longueur du segment [BB'] en fonction de x.
-
Lovile
- Membre Naturel
- Messages: 12
- Enregistré le: 14 Déc 2015, 10:22
-
 par Lovile » 14 Déc 2015, 13:34
par Lovile » 14 Déc 2015, 13:34
Pierrot73 a écrit:Oui, ils valent bien 1, donc VW vaut racine(2).
Malheureusement, ces infos ne vont pas beaucoup t'aider.
Essaie de partir sur cette piste :
Soit la droite (d) horizontale d'équation y = 1. Soit B' le projeté orthogonal de B sur (d) ? Exprime la longueur du segment [BB'] en fonction de x.
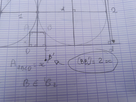

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 14 Déc 2015, 13:38
par Pierrot73 » 14 Déc 2015, 13:38
Lovile a écrit:
Non toujours pas ... Où tracerais-tu la droite (d) d'équation y = 1 ? Et où se trouverait le projeté orthogonal de B sur cette droite ?
Sur ta figure, tu as projeté B sur la droite horizontale d'équation y = -x. Essaies de progresser vers une triangle dont un des côtés correspond au rayon du cercle C2.
-
Lovile
- Membre Naturel
- Messages: 12
- Enregistré le: 14 Déc 2015, 10:22
-
 par Lovile » 14 Déc 2015, 13:47
par Lovile » 14 Déc 2015, 13:47
Pierrot73 a écrit:Non toujours pas ... Où tracerais-tu la droite (d) d'équation y = 1 ? Et où se trouverait le projeté orthogonal de B sur cette droite ?
Sur ta figure, tu as projeté B sur la droite horizontale d'équation y = -x. Essaies de progresser vers une triangle dont un des côtés correspond au rayon du cercle C2.
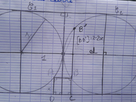

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 14 Déc 2015, 13:54
par Pierrot73 » 14 Déc 2015, 13:54
Lovile a écrit:
On avance
Par contre, ton B' correspond au symétrique de B par rapport à (d), pas à son projeté orthogonal (
aide ).
Au passage, ta valeur de [BB'], tel que ton point B est placé, est bonne. Donc la logique y est

-
Lovile
- Membre Naturel
- Messages: 12
- Enregistré le: 14 Déc 2015, 10:22
-
 par Lovile » 14 Déc 2015, 14:02
par Lovile » 14 Déc 2015, 14:02
Pierrot73 a écrit:On avance
Par contre, ton B' correspond au symétrique de B par rapport à (d), pas à son projeté orthogonal (
aide ).
Au passage, ta valeur de [BB'], tel que ton point B est placé, est bonne. Donc la logique y est

Donc [BB'] =1/2-x ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités



