Déjà choisi bien ton x, tant que t'auras pas choisi ton x une bonne fois pour toute tu ne montreras rien du tout.
Robot t'a dit que tu peux pas te contenter de le prendre dans I (il faut qu'il vérifie autre chose).
Ensuite, une fois cet x choisi, tu dois montrer que pour tout i dans I, il existe a dans A, j dans

, tels que i=ax+j.
"je dois prendre un élément
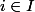
et montrer qu'il existe i qui vérifie une équation tel que i = "élément de xA" + "élément de

" ". c'est vraiment pas clair ça, tu parles de deux i distincts en un seul, fin je comprends pas du tout
Concernant ta citation, toute l'erreur vient du fait que tu ne changes pas de a quand tu écris l'égalité d'ensemble en terme d'éléments:
=A s'écrit: pour tout a dans A, il existe
a' dans A et m dans M, tels que a=a'x+m. aucune raison pour que a=a'...
