Soit la fonction f définie par
1) Réaliser l'étude de la fonction f et dresser son tableau de variation.
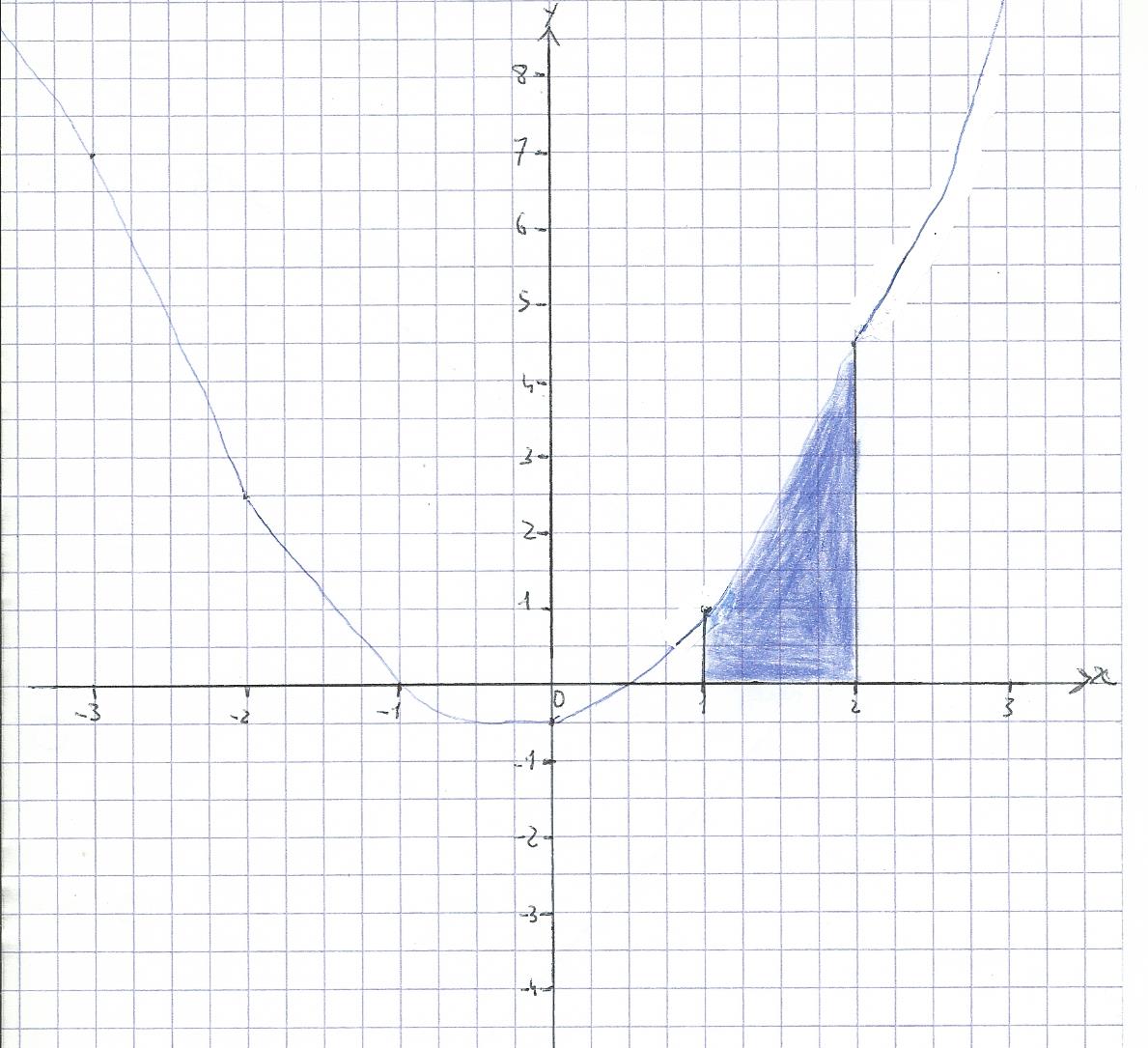
2) Construire Cf en prenant comme unité 2cm sur l'axe des abscisses et 1cm sur l'axe des ordonnées.
3) Calculer l'aire en cm² de la partie du plan situé sur les droites d'équation x=1 et x=2 et l'axe des abscisses et Cf.
1) Domaine de définition.
f est une fonction polynôme du second degré.
On commence par cherché le discriminant.
D'où
Limite
Dérivation
On a f(x) = u(x) + v(x) avec
Donc f'(x) = u'(x) + v'(x) avec
D'où
Variation de f.
On a
Donc pour tout x
f est strictement décroissante de
Et pour tout x
f est strictement croissante de
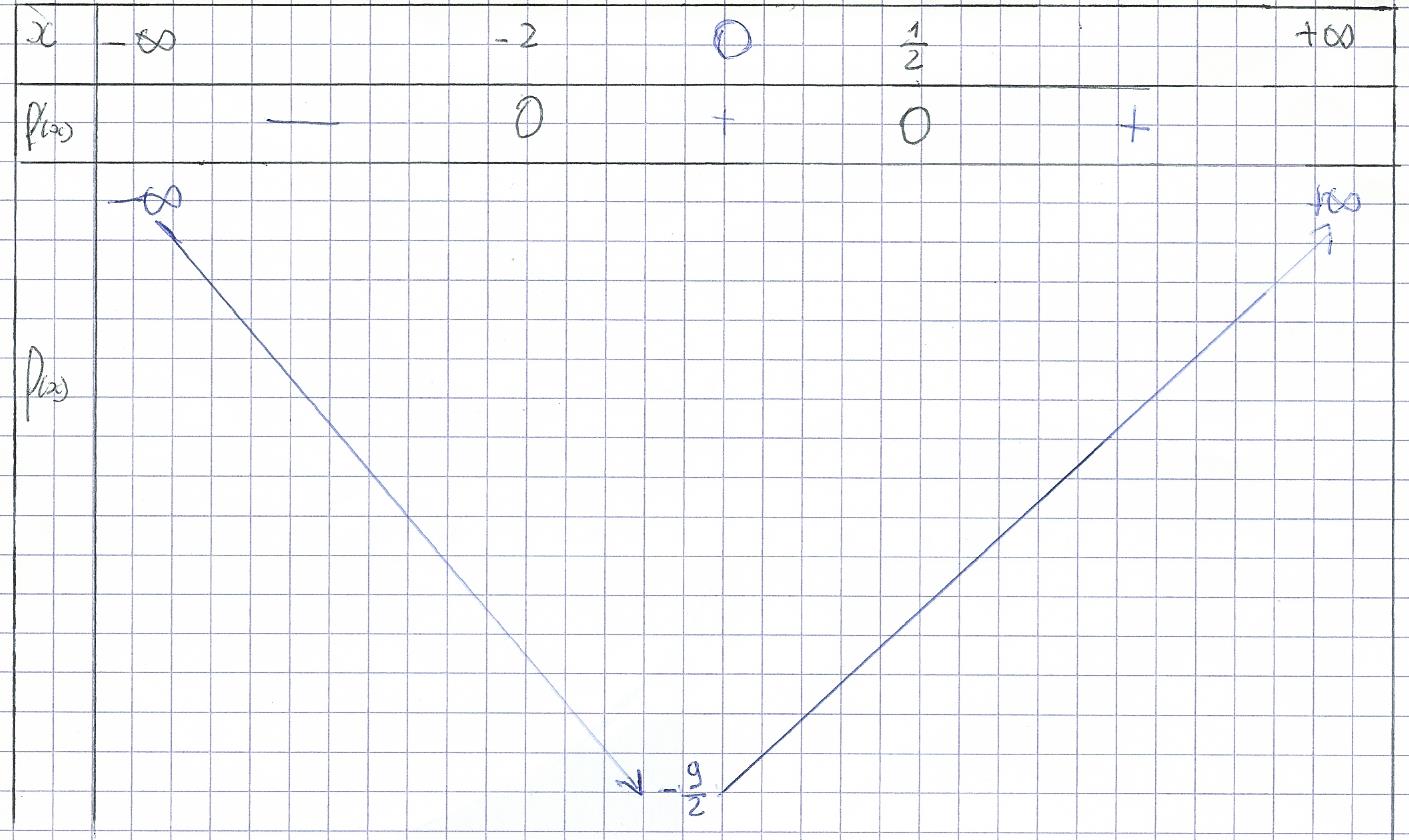
Tableau de variation.
2) Traçage de la courbe.
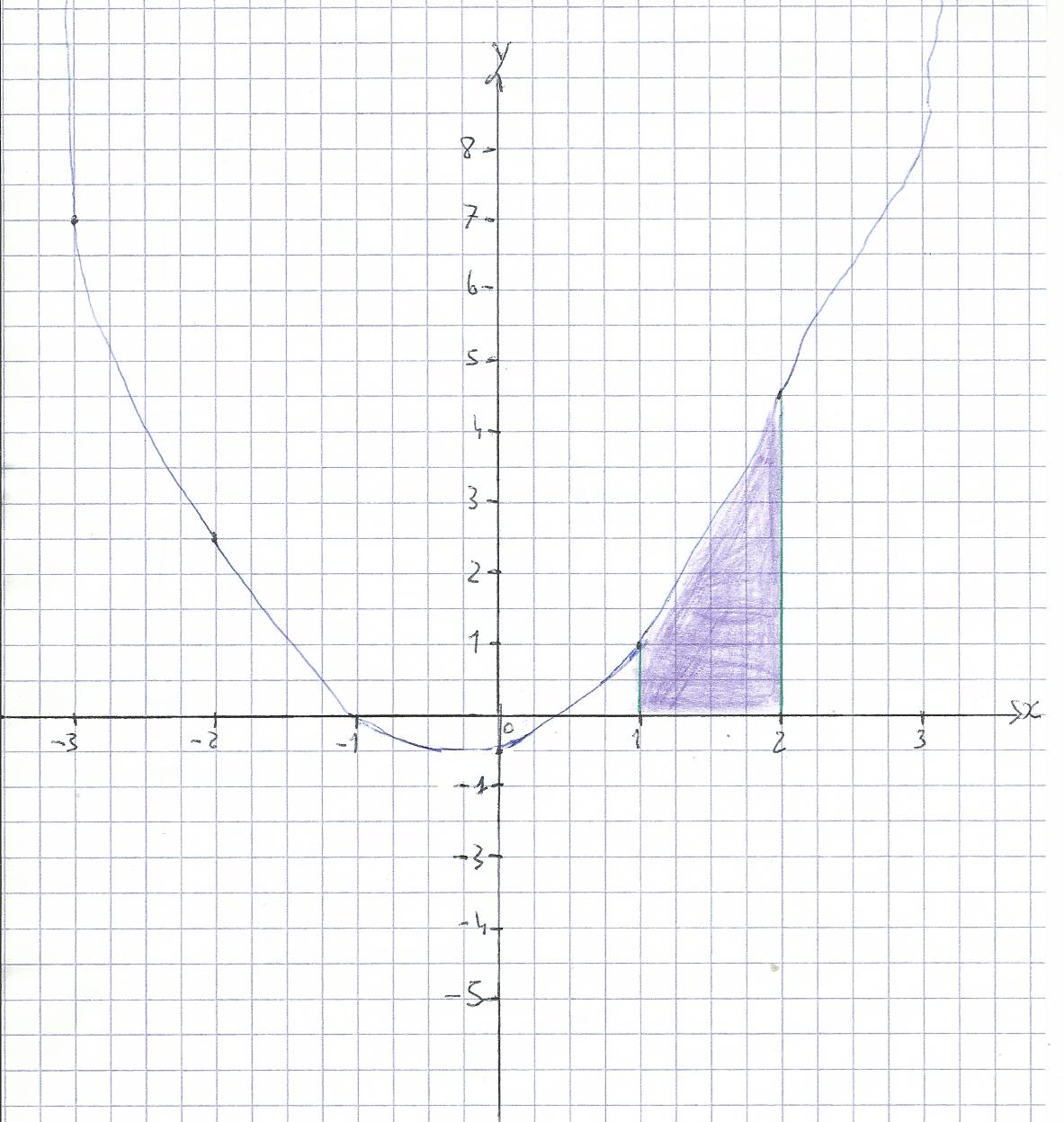
3) Calcul de l'aire.
D'abort on cherche la primitive de
Soit
Je crois, que j'ai fais une erreur sur mon brouillon, je vais tout recommencer.
Est-ce que les limites sont correcte ?
Même question pour la dérivation et la variation de f.
A +