Image d'un cercle par app complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Juin 2015, 10:39
par adamNIDO » 23 Juin 2015, 10:39
paquito a écrit:Non, ça e va pas du tout, tu mets des équivalences en dépit du bon sens, du genre`

????
En plus

, comme

décrit

,

décrit

aussi; tu peut même te limiter à

Tu peux aussi visualiser tout ça sur géogébra; tu définis A(0; 1), B(1; 1) et Z comme image de B dans la rotation de centre A et d'angle a un réel défini sur sur un curseur avec

; puis C(0.5; 0) et Z' l'image de C dans la rotation de centre O et d'angle 1;57-a.
comme j'ai as bien rediger les choses tu peux me proposer votre redaction de solution avec la methode que je fais merci
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Juin 2015, 15:03
par adamNIDO » 23 Juin 2015, 15:03
Bonjour,
S'il vous plait, une rédaction de solution par la methode que j'ai fais
merci d'avance
-
mathelot
 par mathelot » 23 Juin 2015, 15:13
par mathelot » 23 Juin 2015, 15:13
adamNIDO a écrit:Bonjour,
S'il vous plait, une rédaction de solution par la methode que j'ai fais
merci d'avance

on en déduit que l'image par T du cercle de centre A(i) de rayon 1
est le cercle centré à l'origine de rayon 1/2
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Juin 2015, 15:53
par adamNIDO » 23 Juin 2015, 15:53
mathelot a écrit:
on en déduit que l'image par T du cercle de centre A(i) de rayon 1
est le cercle centré à l'origine de rayon 1/2
merci beaucoup mais si possibe davoir une redaction de solution comme celle ci :
On cherche limage de
,1)))
en effet,
 \in T( \mathcal{C}(A(i),1)) \Longleftrightarrow T(z)=\dfrac{i}{2((i+e^{i\theta})-i)}=<br />\dfrac{i}{2(e^{i\theta})}=\dfrac{e^{\frac{i\pi}{2}}}{2(e^{i\theta})}=\dfrac{1}{2}e^{i(\frac{\pi}{2}-\theta)})
finalement
 \in T( \mathcal{C}(A(i),1)) \Longleftrightarrow T(z)=\dfrac{1}{2}e^{i(\pi/2-\theta)})
-
mathelot
 par mathelot » 23 Juin 2015, 15:55
par mathelot » 23 Juin 2015, 15:55
attention
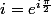
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Juin 2015, 15:58
par adamNIDO » 23 Juin 2015, 15:58
mathelot a écrit:attention
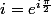
oui merci c'etait faute de frappe mais svp si possible une redaction de solution par la methode que j'ai fais
-
mathelot
 par mathelot » 23 Juin 2015, 16:07
par mathelot » 23 Juin 2015, 16:07
adamNIDO a écrit:finalement
 \in T( \mathcal{C}(A(i),1)) \Longleftrightarrow z'=T(z)=\dfrac{1}{2}e^{i(\pi/2-\theta)})
résultat des courses, quand M appartient au cercle de centre A, de rayon 1
alors M' appartient au cercle de centre O et de rayon 1/2
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Juin 2015, 16:47
par adamNIDO » 23 Juin 2015, 16:47
mathelot a écrit:résultat des courses, quand M appartient au cercle de centre A, de rayon 1
alors M' appartient au cercle de centre O et de rayon 1/2
oui je sais mais imaginer que je dois repondre ca dans un orale ou bien examen ecrit donc je dois rediger bien la solution de A a Z svp tu peux me faire une
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 23 Juin 2015, 18:24
par paquito » 23 Juin 2015, 18:24
adamNIDO a écrit:oui je sais mais imaginer que je dois repondre ca dans un orale ou bien examen ecrit donc je dois rediger bien la solution de A a Z svp tu peux me faire une
La solution tient en une demie ligne, plus c'est maladroit...
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 24 Juin 2015, 10:25
par adamNIDO » 24 Juin 2015, 10:25
paquito a écrit:La solution tient en une demie ligne, plus c'est maladroit...
Bonjour,
merci mais svp ou est ton redaction de solution
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 24 Juin 2015, 11:27
par paquito » 24 Juin 2015, 11:27
adamNIDO a écrit:Bonjour,
merci mais svp ou est ton redaction de solution
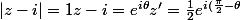})
d'où
|\in C(A,1)M'(z')\in C(O,\frac{1}{2}))
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 24 Juin 2015, 16:40
par adamNIDO » 24 Juin 2015, 16:40
paquito a écrit: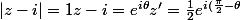})
d'où
|\in C(A,1)M'(z')\in C(O,\frac{1}{2}))
merci beaucoup pour votre aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
????
, comme
décrit
,
décrit
aussi; tu peut même te limiter à
; puis C(0.5; 0) et Z' l'image de C dans la rotation de centre O et d'angle 1;57-a.
