Equation Différentielle avec second membre

[ArtyB]

Bonjour,
Je souhaiterais avoir de l'aide pour résoudre cette equation differentielle. Il faut tout d'abord trouver une solution generale de l'equation homogène associée de la forme ke^A(x) avec A la primitive de a tel que y'=ay et ensuite il faut trouver une solution particulière de l'equation avec le methode de variation de la constante je suppose mais je n'arrive pas à l'appliquer dans ce cas précis. Si quelqu'un pouvait m'aider, cela me rendrait un grand service.
Merci !

cos(x)*y'-(x²*cos(x)-sin(x))*y=e^[(x^3)/3]

[mathelot]

bjr,

l'équation est affine (linéaire sans le second membre)

on résout formellement l'équation homogène:





le membre de gauche se primitive en

cf. livres de Valiron "Théorie des fonctions" et "Équations fonctionnelles"

lien

le livre de Valiron, dont je ne sais même pas s'il n'a pas été publié avant-guerre,
concerne la solution exacte des équas diff. Par contre, à l'époque moderne,
on cherche plutôt des solutions algorithmiques (systèmes dynamiques)
(méthode de Runge-Kutta, schémas à un pas, à deux pas, travaux de Raviart, de Lyons..)
sans trop se soucier des formules closes donnant les courbes intégrales.
tout ça pour dire que le point de vue a changé avec l'apparition des ordinateurs
et que les équations de Riccati et autres sont là "pour mémoire",
les matheu(ses) s'occupent plutôt d'analyse numérique que de résolutions exactes,
ce qui a donné le "la" de cette nouvelle approche, sont les travaux de Poincaré de 1900 à propos de
la stabilité du système solaire, inaugurant les systèmes dynamiques.

[ArtyB]

Merci de votre réponse,
Je suis d'accord avec la fraction y'/y mais à quoi cela sert il ?
De même la primitive de ln(y) je ne la vois pas dans le membre de gauche et je ne vois pas comment résoudre l'équation avec ces éléments, pourriez vous développer votre raisonnement ?

[mathelot]

peux tu primitiver le membre de droite, svp (variable x) ?
après on égalise deux primitives sur un intervalle, modulo une constante additive puis on passe à l'exponentielle modulo une constante multiplicative



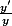est la dérivée de

est la dérivée de ..... ?

que peut on dire de deux fonctions continues dont les dérivées sont égales sur un même intervalle
de définition ?

[mathelot]

la constante dépend de l'intervalle (a priori de longueur pi)

[wally68]

bonjour,
Pouvez-vous m'aider ar j'ai une équation diérentielle a faire et je n'y arrive pas:
y'(t)=2y2(t)-4y(t)/y(t)+2
existence des solutions, solutions stationnaire, sense de variation des solutions, .....

[mathelot]

la variation de la constante donne





de plus, le domaine des solutions sont des intervalles disjoints de longueur

Dans la phase de synthèse du raisonnement, on s'intéresse aux raccords de classe C1

[mathelot]

dans la phase de synthèse, on voit que les solutions sont définies sur R
et donc qu'il a été possible de raccorder de façon C1 les différents intervalles
en simplifiant le quotient

NB: le raccord est dit de classe C1 quand le point de raccordement est une fausse
singularité, que le calcul des limites donne la continuité , la dérivabilité de y et la continuité de la dérivée y', ce qui est le cas ici.

[ArtyB]

"on égalise deux primitives sur un intervalle, modulo une constante additive puis on passe à l'exponentielle modulo une constante multiplicative"
Je ne comprends malheureusement pas ce que cela veut dire.


x-tan(x) est la dérivée de (x^3)/3+0,5 *ln(sin2(x);)1)

"que peut on dire de deux fonctions continues dont les dérivées sont égales sur un même intervalle de définition ?"
-> Que ce sont les mêmes fonctions ?

"la constante dépend de l'intervalle (a priori de longueur pi)" c'est à dire ?

Comment trouver la variation de la constante ?

"phase de synthèse" qu'est-ce donc ?


Visiblement je n'ai pas le vocabulaire requis pour comprendre vos explications...

[mathelot]

"on égalise deux primitives sur un intervalle, modulo une constante additive puis on passe à l'exponentielle modulo une constante multiplicative"
Je ne comprends malheureusement pas ce que cela veut dire.


x-tan(x) est la dérivée de (x^3)/3+0,5 *ln(sin2(x);)1)
Ln(|cos(x)|) semble une écriture plus simple

"que peut on dire de deux fonctions continues dont les dérivées sont égales sur un même intervalle de définition ?"
-> Que ce sont les mêmes fonctions ?
leur différence est constante
"la constante dépend de l'intervalle (a priori de longueur pi)" c'est à dire ?
on a écrit Ln(|cos(x)|) qui n'est pas valide sur R tout entier
Comment trouver la variation de la constante ?
en écrivant K(x) à la place de K.

"phase de synthèse" qu'est-ce donc ?
le raisonnement se fait par analyse- synthèse
exemple:
3x+1=0
si l'équation admet une solution, alors nécessairement (analyse):
x=-1/3
réciproquement (synthèse) -1/3 est solution de l'équation

Visiblement je n'ai pas le vocabulaire requis pour comprendre vos explications...
reste plus qu'à comprendre les équations sans les explications

(-sin(x)/cos(x)) est de la forme u'/u, nan ?

....................

[Black Jack]

"on égalise deux primitives sur un intervalle, modulo une constante additive puis on passe à l'exponentielle modulo une constante multiplicative"
Je ne comprends malheureusement pas ce que cela veut dire.


x-tan(x) est la dérivée de (x^3)/3+0,5 *ln(sin2(x);)1)

"que peut on dire de deux fonctions continues dont les dérivées sont égales sur un même intervalle de définition ?"
-> Que ce sont les mêmes fonctions ?

"la constante dépend de l'intervalle (a priori de longueur pi)" c'est à dire ?

Comment trouver la variation de la constante ?

"phase de synthèse" qu'est-ce donc ?


Visiblement je n'ai pas le vocabulaire requis pour comprendre vos explications...

y'/y = x² - sin(x)/cos(x) (1)

On intégre :

ln|k.y| = x³/3 + ln|cos(x)|

|ky| = e^(x³/3 + ln|cos(x)|)

|ky| = e^(x³/3) * e^(ln|cos(x)|)

ky = cos(x) * e^(x³/3)

et en posant k = 1/C :

y = C.cos(x) * e^(x³/3)

Avec C une constante réelle quelconque (qui peut prendre des valeurs différentes quand on change de "partie" du domaine de définition qui est non connexe (puisque cos(x) = 0 est interdit dans (1) ))

...

:zen:

[mathelot]

|ky| = e^(x³/3) * e^(ln|cos(x)|)

ky = cos(x) * e^(x³/3)

tu peux expliciter ce passage (on se débarasse des valeurs absolues), je sais
que ça marche mais je sais pas faire...

si, ça y est, j'ai compris. On résout sur des intervalles où y ne s'annule pas et comme
elle y est continue, elle garde un signe constant. :hein:

[ArtyB]

Bon, au final j'ai essayé de comprendre vainement ce que vous avez voulu me dire et j'ai tout repris ce que je savais et j'ai fait la chose suivante:

cos(x)*y'-(x²*cos(x)-sin(x))*y=e^[(x^3)/3]

on nomme b(x) le second membre (ie (e^(x^3)/3)/cos(x) )

1)on cherche une solution generale de l'equation homogene associée:
y'=y*(x² - sin(x)/cos(x) )
y'=y*a(x)
la solution generale est de la forme ke^A(x) avec k constante et A primitive de a
on remarque qu'une primitive de a est A(x)=(x^3)/3 +ln(cos(x))
d'où y=e^A(x)=e^[ (x^3)/3 + ln(cos(x)) ]

2) on cherche une solution paritculière y1 de l'equation avec second membre grâce à la méthode de variation de la constante
y1=g(x) e^A(x)
avec g'(x)=b(x) e^-A(x)
g'(x)=...
g'(x)=1/cos²(x)

On remarque que g'(x)=tan'(x) donc tan(x) est une primitive de g'(x)
On prend g(x)=tan(x)
alors y1=tan(x)e^[ (x^3)/3 + ln(cos(x)) ]

3) La solution générale de l'équation de second degré est la somme de la solution generale de l'equation homogene associée et de la solution particulière
Y=y+y1= (1+ tan(x) )* e^[ (x^3)/3 + ln(cos(x)) ]

Qu'en pensez vous ?

[mathelot]

Bien joué!

alors y1=tan(x)e^[ (x^3)/3 + ln(cos(x)) ]

se simplifie car exp( ln(a))=a

[ArtyB]

Chouette, j'ai compris alors !
Ah oui merci, je n'avais même pas fait attention...

[mathelot]

regarde mon post de 10H09 intitulé "au final". Il y a là la forme générale d'une solution.

[ArtyB]

Je ressors vite fait ce sujet, la solution finale doit elle être la somme de la solution générale et de la solution particulière ou juste la solution trouvée par méthode de la variation de constante ?

Parce que je vérifiais par hasard ma réponse:
y=e^((x^3)/3)*cos(x)*(1+tan(x))
et ça ne marchait pas alors que
y=e^((x^3)/3)*cos(x)*(tan(x)) fonctionne

[mathelot]

Je ressors vite fait ce sujet, la solution finale doit elle être la somme de la solution générale du système homogène et de la solution particulière

oui, c'est exact.

récapitulons
le système homogène a pour solution générale
on fait varier la constante avec K(x)

on trouve

solution générale de l'équa.diff:



L'ensemble des solutions a une structure affine avec pour e.v les fonctions réelles définies
sur
est une fonction particulière,ie, un "point" de l'espace affine

est une droite vectorielle.

[ArtyB]

Le K de la solution générale n'a rien à voir avec le K(x) de la variation de la constante si ?

Et pour la variation de la constante je ne trouve pas tan(x)+lambda mais
tan(x)*e^((x^3)/3)*cos(x)
de même à la fin je ne trouve pas du tout ça:

1)on cherche une solution generale de l'equation homogene associée:
y'=y*(x² - sin(x)/cos(x) )
y'=y*a(x)
la solution generale est de la forme ke^A(x) avec k constante et A primitive de a
on remarque qu'une primitive de a est A(x)=(x^3)/3 +ln(cos(x))
d'où y=e^A(x)=e^[ (x^3)/3 + ln(cos(x)) ]

2) on cherche une solution paritculière y1 de l'equation avec second membre grâce à la méthode de variation de la constante
y1=g(x) e^A(x)
avec g'(x)=b(x) e^-A(x)
g'(x)=...
g'(x)=1/cos²(x)

On remarque que g'(x)=tan'(x) donc tan(x) est une primitive de g'(x)
On prend g(x)=tan(x)
alors y1=tan(x)e^[ (x^3)/3 + ln(cos(x)) ]

3) La solution générale de l'équation de second degré est la somme de la solution generale de l'equation homogene associée et de la solution particulière
Y=y+y1= (1+ tan(x) )* e^[ (x^3)/3 + ln(cos(x))

[mathelot]

Le K de la solution générale n'a rien à voir avec le K(x) de la variation de la constante si ?

bah si. La variation de la constante donne une solution de la forme
et la constante C vient jouer le rôle de l'ancienne constante K.

Et pour la variation de la constante je ne trouve pas tan(x)+lambda mais
tan(x)*e^((x^3)/3)*cos(x)
de même à la fin je ne trouve pas du tout ça:

1)on cherche une solution generale de l'equation homogene associée:
y'=y*(x² - sin(x)/cos(x) )
y'=y*a(x)
la solution generale est de la forme ke^A(x) avec k constante et A primitive de a
on remarque qu'une primitive de a est A(x)=(x^3)/3 +ln(cos(x))
d'où y=e^A(x)=e^[ (x^3)/3 + ln(cos(x)) ] (2)
l'écriture (2) se simplifie.

2) on cherche une solution paritculière y1 de l'equation avec second membre grâce à la méthode de variation de la constante
y1=g(x) e^A(x)
avec g'(x)=b(x) e^-A(x)
g'(x)=...
g'(x)=1/cos²(x)

On remarque que g'(x)=tan'(x) donc tan(x) est une primitive de g'(x)
On prend g(x)=tan(x)+C ne pas oublier la constante

alors y1=(tan(x)+\lambda)e^[ (x^3)/3 + ln(cos(x)) ]