Système d'équation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Bloodthirsty
- Membre Naturel
- Messages: 44
- Enregistré le: 03 Déc 2012, 15:14
-
 par Bloodthirsty » 04 Fév 2015, 17:37
par Bloodthirsty » 04 Fév 2015, 17:37
Bonjour, j'ai un système d'équation à résoudre mais je bloque :
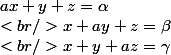
Après quelques calculs je bloque à partir de là :
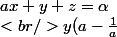 + z(1 - \frac{1}{a}) = \beta - \frac{\alpha}{a} \\<br /> y(1 - \frac{1}{a}) + z(a - \frac{1}{a}) = \gamma - \frac{\alpha}{a})
J'essaye d'éliminer le y sur la 3ème ligne mais je vois pas comment...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Fév 2015, 17:41
par zygomatique » 04 Fév 2015, 17:41
salut
ha bon .... tu divises allégrement par a comme ça ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Bloodthirsty
- Membre Naturel
- Messages: 44
- Enregistré le: 03 Déc 2012, 15:14
-
 par Bloodthirsty » 04 Fév 2015, 17:57
par Bloodthirsty » 04 Fév 2015, 17:57
J'aurais du mettre pour
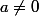
avant...

-
WillyCagnes
- Membre Transcendant
- Messages: 3753
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 04 Fév 2015, 18:05
par WillyCagnes » 04 Fév 2015, 18:05
bsr
si tu additionnes les 3 equations, tu obtiens
alpha+beta+gamma=(2+a)(x+y+z)
donc avec a<>-2
x+y+z= (alpha+beta+gamma)/(2+a)
puis on a
ax+y+z=alpha
la difference tu obtiens
x(1-a)=(alpha+beta+gamma)/(2+a) -alpha
avec a<>1
d'ou x=[(alpha+beta+gamma)/(2+a) -alpha]/(1-a)
et ensuite tu pourras calculer y et z avec la même logique

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Fév 2015, 18:29
par zygomatique » 04 Fév 2015, 18:29
on additionne membre à membre pour avoir (a + 2)(x + y + z) = u + v + w
1/ a + 2 = 0 alors :
1/a/ ... ?
1/b/ ... ?
2/ a + 2 <> 0
alors .... ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 04 Fév 2015, 19:29
par chan79 » 04 Fév 2015, 19:29
Envisager à part les cas a=1 et a=-2
Sinon, il y a une seule solution pour (x,y,z)
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 04 Fév 2015, 19:47
par fibonacci » 04 Fév 2015, 19:47
Bonsoir;
c'est la méthode de WillyCagnes qui est la plus simple à mettre en oeuvre,
on peut continuer avec ce que tu as fait en égalant les coefficients de y et par différence tu obtiens z
\quad y(a - \frac{1}<br />{a})(1 - \frac{1}<br />{a}) + z(1 - \frac{1}<br />{a})(1 - \frac{1}<br />{a}) = (\beta - \frac{\alpha }<br />{a})(1 - \frac{1}<br />{a}) \hfill \\)
2)
(a - \frac{1}<br />{a}) + z(a - \frac{1}<br />{a})(a - \frac{1}<br />{a}) = - (\gamma - \frac{\alpha }<br />{a})(a - \frac{1}<br />{a}) \hfill \\)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Fév 2015, 19:57
par zygomatique » 04 Fév 2015, 19:57
le problème n'est pas de résoudre .... une machine le fait formellement ....
le problème c'est l'existence de la ou des solutions ...
ax + y + z = u (1)
x + ay + z = v (2)
x + y + az = w (3)
(a + 2)(x + y + z) = u + v + w <=> x + y + z = (u + v + w)/(2 + a) (4)
(1) - (4)
(2) - (4)
(3) - (4)
donnent immédiatement x, y, et z et font apparaître le cas a = 1 relevé par chan79
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
vingtdieux
- Membre Relatif
- Messages: 196
- Enregistré le: 27 Mai 2010, 22:22
-
 par vingtdieux » 04 Fév 2015, 23:51
par vingtdieux » 04 Fév 2015, 23:51
Possible résolution par la méthode de Cramer. Le déterminant au dénominateur fait aussi apparaitre les cas a=1 et a=-2
-
Bloodthirsty
- Membre Naturel
- Messages: 44
- Enregistré le: 03 Déc 2012, 15:14
-
 par Bloodthirsty » 05 Fév 2015, 15:13
par Bloodthirsty » 05 Fév 2015, 15:13
Ok j'ai compris, merci pour votre aide !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités