Polynome premiers entre eux
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ezril13
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Sep 2013, 14:08
-
 par ezril13 » 14 Déc 2014, 19:21
par ezril13 » 14 Déc 2014, 19:21
Bonjour,
Ce résultat a été utiliser en cour mais je n'arrive pas à le démontrer.
Soit A et B deux polynomes dans
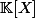
 = 1\Rightarrow pgcd(A^2,B^2) = 1)
Ce que j'ai essayé :
on suppose
 = 1)
Soit D tel que

mais je ne vois pas comment démontrer que


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Déc 2014, 19:44
par Ben314 » 14 Déc 2014, 19:44
Salut,
Pour toutes les preuves de ce type, on suppose en plus que D est irréductible.
Donc, par exemple, de D|A²=AxA, tu déduit que D|A (dans un anneau euclidien, si un irréductible divise un produit, il divise l'un des deux)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 14 Déc 2014, 19:50
par zygomatique » 14 Déc 2014, 19:50
salut
il ne me semble pas nécessaire d'avoir cette condition il me semble ....
si d divise a et b alors d divise aa et bb
si pgcd(a, b) = 1 alors d divise 1
donc d est scalaire donc pgcd(aa, bb) = 1 ...
non ?
EDIT : Ben non effectivement :marteau: .. j'suis fatigué ... j'vais allé manger ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Déc 2014, 20:08
par Ben314 » 14 Déc 2014, 20:08
Ben... non..
Le but est de montrer que,
si pgcd(A,B)=1 alors pgcd(A²,B²)=1 et pas la réciproque (qui est bien plus triviale).
Et pour
montrer que pgcd(A²,B²)=1, tu doit partir d'un D qui divise A² et B² (et pas d'un D qui divise A et B) alors que ta première phrase commence par "si D divise A et B alors..."
En fait, on peut aussi le faire avec Bézout en vérifiant que :
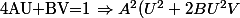+B^2(V^2+2AUV^2)=1)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ezril13
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Sep 2013, 14:08
-
 par ezril13 » 14 Déc 2014, 20:36
par ezril13 » 14 Déc 2014, 20:36
Je n'arrive pas à obtenir 1 avec bézout.
Je dévellope et j'obtiens :
)
C'est donc égale à 1 ssi
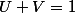
?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Déc 2014, 20:40
par Ben314 » 14 Déc 2014, 20:40
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités