Arithmétique des polynômes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Charmander
- Membre Naturel
- Messages: 90
- Enregistré le: 13 Oct 2013, 16:22
-
 par Charmander » 06 Déc 2014, 18:44
par Charmander » 06 Déc 2014, 18:44
Bonsoir,
Soit n entier naturel non nul et
\in\mathbb{N}^n)
tel que, pour tout
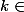
{0,...,n-1},

.
Montrer que
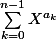
est divisible par
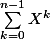
ça fait un moment que j'essaie, je n'y arrive pas. J'ai essayé de poser la division ou raisonner modulo
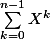
mais ça n'a pas l'air de marcher. Quelqu'un peut m'aider ? Merci

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 06 Déc 2014, 18:53
par zygomatique » 06 Déc 2014, 18:53
salut
et si on prend a_k = k ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Déc 2014, 19:09
par Ben314 » 06 Déc 2014, 19:09
Salut,
1) Quelles sont les racines (dans C) de
=\sum_{k=0}^{n-1} X^k)
?
2) Quels sont leur ordre de multiplicité ?
3) Sont-ce des racines de
=\sum_{k=0}^{n-1} X^{a_k})
?
4) Conclusion.
Edit : Autre méthode (plus "bébète")
Si
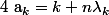
alors
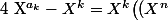^{\lambda_k}-1\big)<br />=X^k\big(X^n-1)(\big(X^n)^{\lambda_k-1}+(X^n)^{\lambda_k-2}++...+X^n+1\big))
est divisible par

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Déc 2014, 19:15
par Ben314 » 06 Déc 2014, 19:15
Salut,
1) Quelles sont les racines (dans C) de
=\sum_{k=0}^{n-1} X^k)
?
2) Quels sont leur ordre de multiplicité ?
3) Sont-ce des racines de
=\sum_{k=0}^{n-1} X^{a_k})
?
4) Conclusion.
Edit : Autre méthode (plus "bébète")
Si
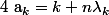
alors
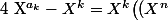^{\lambda_k}-1\big)<br />=X^k\big(X^n-1)(\big(X^n)^{\lambda_k-1}+(X^n)^{\lambda_k-2}++...+X^n+1\big))
est divisible par

donc
-Q(X)\)
est divisible par

lui même divisible par
)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Charmander
- Membre Naturel
- Messages: 90
- Enregistré le: 13 Oct 2013, 16:22
-
 par Charmander » 06 Déc 2014, 19:32
par Charmander » 06 Déc 2014, 19:32
Bonsoir,
Ce sont les racines n-ièmes non-triviales de l'unité, elles sont distinctes donc d'ordre 1, donc il suffit de vérifier qu'ils sont aussi racines de P ce qui est vrai donc Q divise P.
Merci beaucoup !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités