BiancoAngelo a écrit:=\lim_{n\to\infty}\Big(\lim_{m\to\infty}\big(\cos(n!\pi x)\big)^{2m}\Big))
ou
=\lim_{m\to\infty}\Big(\lim_{n\to\infty}\big(\cos(n!\pi x)\big)^{2m}\Big))
Non c'est bien la première écriture, et elle est trés différente de la deuxième.
Dans le premier cas, la "limite de limite" existe pour tout réel x, alors que dans le deuxième cas, la limite n'existe
que pour les x rationnelsExplication :
Quelque soit le réel x et l'entier n (fixés tout les deux), on a
\big)^2\in[0,1]\)
et le résultat classique concernant les suites géométriques te dit que, lorsque m tend vers +oo

tend vers 0
sauf si q=1 où

tend évidement vers 1.
De plus,
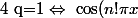=\pm 1\ \Leftrightarrow\ n!\pi x=k\pi\ (k\in{\mathbb Z})\ \Leftrightarrow\ n! x\in{\mathbb Z})
Bilan :
=\lim_{m\to\infty}\big(\cos(n!\pi x)\big)^{2m}=\left\{\matrix{1\text{ si }n! x\in{\mathbb Z}\cr 0\text{ sinon }\ \ \ \ \ \ })
Reste à évaluer
=\lim_{n\to\infty}f_n(x))
- Si

alors, pour tout

on a

donc
=1)
et on en déduit que
=1)
- Si

alors, pour tout

, on a

donc
=0)
et on en déduit que
=0)
Si tu cherche a calculer les limites "dans l'autre sens", en commençant par
\big)^{2m})
(pour m et x fixés) alors, si x est rationnel la limite existe et vaut 1 mais, lorsque x n'est pas un rationnel, la limite n'existe pas forcément (peut-être pour certains non rationnels particulier, mais pas pour tous)
P.S. Je pense (peut-être à tort) que c'est une question difficile de savoir pour quels non rationnels la limite en question existe...
