Voilà l'affaire : Je rentre en prépa PCSI l'année prochaine et j'ai un devoir de vacances de 3 exercices : j'en ai fait deux relativement facilement , mais le troisième me pose pas mal de problèmes : voici le PDF , c'est l'exercice n°1 , partie A) ===> [HTML]http://www.prepa-cpe.fr/IMG/UserFiles/Files/Rentr%C3%A9e%202014/Math%20-%20Devoir%20%202014%20Sup.pdf[/HTML]
Je bloque direct à la question 1 , et je préfère comprendre (Je sais qu'on peut la sauter) , étant donné que je crains démarrer du mauvais pied si je n'arrive pas a comprendre ce devoir de vacances de A à Z. Je vois pas comment transformer l'expression de droite pour arriver a celle de gauche ou vice versa ... Faut-il que je transforme ça en une suite/somme de suite ? (les suites et surtout les SOMMES de suites ont toujours été ma seule faiblesse en maths de lycée).
Et ayant regardé l'exercice , je n'ai pas non plus réussi a transformer cette somme en primitive de la dérivée de Un (car l'expression demandée en 2) est Un - primitive , ce qui veut dire que il faut que je fasse la primitive et retrouver Un - le machin au final)
Il est relativement tard , donc je vais attendre 30 minutes en cas de réponse immédiate , mais je dormirai ensuite jusqu'à 12h demain (1er août).
Merci de votre aide.
Suites / Primitives. Niveau supposé TS
32 messages
- Page 1 sur 2 - 1, 2
par ampholyte » 01 Aoû 2014, 07:45
Bonjour,
Pour ce genre de question, si tu ne vois absolument pas comment faire, il faut essayer de chercher la simplificité.
Tu as une expression de la forme :
^n t^{2n}) - \frac{1}{1 + t^2})
Pourquoi ne pas essayer de mettre au même dénominateur pour voir ce qui se passe ?
^nt^{2n})(1 + t^2) -1 }{1 + t^2})
On développe (je ne garde que le numérateur pour simplifier l'explication)
^nt^{2n})(1 + t^2) -1 = (1 - t^2 + t^4 - \text{...} + (-1)^nt^{2n}) + (t^2 - t^4 + t^6 - \text{...} (-1)^nt^{2n + 2}) - 1)
A partir d'ici on voit parfaitement que cela peut se simplifier en additionnant tout.
Est-ce plus clair ?
Pour la preuve tu peux peut-être essayer de mettre tout ça sous une somme :
^kt^{2k} = 1 - t^2 + t^4 - t^6 + \text{...} + (-1)^nt^{2n})
Pour ce genre de question, si tu ne vois absolument pas comment faire, il faut essayer de chercher la simplificité.
Tu as une expression de la forme :
Pourquoi ne pas essayer de mettre au même dénominateur pour voir ce qui se passe ?
On développe (je ne garde que le numérateur pour simplifier l'explication)
A partir d'ici on voit parfaitement que cela peut se simplifier en additionnant tout.
Est-ce plus clair ?
Pour la preuve tu peux peut-être essayer de mettre tout ça sous une somme :
par paquito » 01 Aoû 2014, 07:57
Bonjour, l'astuce est de voir que ^nt^{2n})
constitue la suite de 
termes consécutifs d'une suite géométrique de raison 
; ^{n+1}=-1(-1)^n)
d'où^k=\frac{1+(-1)^n t^{2n+2}}{1+t^2})
et
^k-\frac{1}{1+t^2}=\frac{(-1)^n t^{2n+2}}{1+t^2})
et en intégrant cette égallité tu obtiens bien:
^n t^{2n+2}}{1+t^2})
la qestion 3) est facile.
B) la fonction
étant continue sur R, F est la primitive de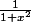 
qui s'annule pour x=0, donc =\frac{1}{1+x^2})
.
La suite est raisonnable. Il faut juste penser que=1)
d'où
la qestion 3) est facile.
B) la fonction
La suite est raisonnable. Il faut juste penser que
par zzzzzzzzz » 01 Aoû 2014, 17:35
Merci de vos réponses ! Il y a toujours un point que je ne comprends pas.
Je sais intégrer une égalité , mais je n'ai jamais intégré une somme de suite géométrique , et je ne vois pas comment ça donne Un .. c'est peut-être un point de cours hors programme TS ? Ou c'est juste évident si j'y réfléchis , je vais essayer de trouver par moi même...
Je sais intégrer une égalité , mais je n'ai jamais intégré une somme de suite géométrique , et je ne vois pas comment ça donne Un .. c'est peut-être un point de cours hors programme TS ? Ou c'est juste évident si j'y réfléchis , je vais essayer de trouver par moi même...
par paquito » 01 Aoû 2014, 17:46
ampholyte a écrit:Bonjour,
Pour ce genre de question, si tu ne vois absolument pas comment faire, il faut essayer de chercher la simplificité.
Tu as une expression de la forme :
Pourquoi ne pas essayer de mettre au même dénominateur pour voir ce qui se passe ?
On développe (je ne garde que le numérateur pour simplifier l'explication)
A partir d'ici on voit parfaitement que cela peut se simplifier en additionnant tout.
Est-ce plus clair ?
Pour la preuve tu peux peut-être essayer de mettre tout ça sous une somme :
C'est pas clair du tout! Tu compliques tout! Tout ça pour finir sur une bonne série géométrique!
par zzzzzzzzz » 01 Aoû 2014, 18:07
Re-Bonjour paquito. tu pourrais m'expliquer comment la somme géométrique se transforme en U(n) lorsqu'on l'intègre de 0 à 1 ?? J'ai pas vu ça en lycée , malgré de nombreux exos... C'est probablement un dérivé du cours , mais que je n'ai jamais rencontré :(
par zzzzzzzzz » 01 Aoû 2014, 19:50
Je ne comprends toujours pas comment ^nt^{2n+2}}{1+t^2})
Vous pourriez m'aider en développant le calcul pas à pas et en me montrant comment calculer cette intégrale ?
Vous pourriez m'aider en développant le calcul pas à pas et en me montrant comment calculer cette intégrale ?
par Mikihisa » 01 Aoû 2014, 20:37
Alors ce n'est pas exactement ce qu'on te demande, si tu fais référence a la question 2)
On te demande de déduire que^n\int_0^1\frac{t^{2n+2}}{1+t^2}dt)
Je veux bien accepter que c'est exactement la même chose, mais si on te le pose sous cette forme y'a une raison
Pour répondre a la question il suffit juste d'intégrer l'égalité de 1)
Quelles sont les primitive de
?
Pour répondre a ta question ( qui n'est pas la question de l'exercice je précise )
Tu ne sais pas calculer cette intégrale avec le niveau TS et est tout a fait normal :
+K)
Et pour
il faut remarquer que (t^{2n}-t^{2n-2}+...\pm 1)\pm 1)
Et donc que
(un truc comme ça ) et tu sais intégrer tout les membre de la somme.
Mais encore une fois ce n'est pas du tout dans tes corde (division euclidienne des polynome ) et ce n'est pas le but de l'exercice.
On te demande de déduire que
Je veux bien accepter que c'est exactement la même chose, mais si on te le pose sous cette forme y'a une raison
Pour répondre a la question il suffit juste d'intégrer l'égalité de 1)
Quelles sont les primitive de
Pour répondre a ta question ( qui n'est pas la question de l'exercice je précise )
Tu ne sais pas calculer cette intégrale avec le niveau TS et est tout a fait normal :
Et pour
Et donc que
Mais encore une fois ce n'est pas du tout dans tes corde (division euclidienne des polynome ) et ce n'est pas le but de l'exercice.
par zzzzzzzzz » 01 Aoû 2014, 20:58
t^3/3 et t^5/5 , et ça se rapproche des premiers termes de la somme qu'est U(n) , je cherche encore comment virer chaque t^n de là ...
par zzzzzzzzz » 01 Aoû 2014, 20:59
ahhh mais oui ! c'est la primitive de 0 à 1 donc ça devient U(n) exactement quand on développe ! Merci :D
par Mikihisa » 01 Aoû 2014, 21:02
J'ai ajouter une petite note en édit car tu demandais "comment calculer l'intégrale", mais je répète que ce n'est pas le but de l'exercice.
par zzzzzzzzz » 01 Aoû 2014, 21:10
Oui merci , j'attaque la partie B) 2) avec u(x) , première fois de ma vie que je vois tan(x) en action , ça va pas aller vite :p
par Mikihisa » 01 Aoû 2014, 21:27
Bon courage, ça devrais aller c'est assez instinctif.
Tu auras donc constater que F(x) =
(la primitive) est la fonction réciproque de tan(x) (on a arctan(tan x)=x), c'est la mesure en radian de l'angle dont la tangente vaux x.
On définie de la même manière arccos(x) et arcsin(x).
Et j'ajoute enfin que ces fonctions interviennent très souvent lorsque l'on cherche a calculer les primitive des fonction rationnelles, mais j'en dit pas plus.
Tu auras donc constater que F(x) =
On définie de la même manière arccos(x) et arcsin(x).
Et j'ajoute enfin que ces fonctions interviennent très souvent lorsque l'on cherche a calculer les primitive des fonction rationnelles, mais j'en dit pas plus.
par zzzzzzzzz » 01 Aoû 2014, 21:29
Je n'ai AUCUNE idée de comment traiter la partie B) 2) a) et b) .... Ah , c'est instinctif ...
par Mikihisa » 01 Aoû 2014, 21:40
Ah !
Bah c'est pas difficile pourtant, tu sais d'après le théorème fondamental de l'analyse que F(x)=
est une primitive de =\frac{1}{1+t^2})
car f est continue sur [0;1], donc tu sais que F est dérivable et F'(x)=f(x), ça c'était la question 1).
Bah pour la question 2)a) il suffit de voir u(x) comme compose de fonction dérivable.
Et pour b) tu sais que tan(0) = 0 et l'intégrale une fonction sur un intervalle vide (i.e. Entre 0 et 0 par exemple est forcément nulle, toi qui est
Physicien, ça serait l'aire d'un segment ^^
Bah c'est pas difficile pourtant, tu sais d'après le théorème fondamental de l'analyse que F(x)=
Bah pour la question 2)a) il suffit de voir u(x) comme compose de fonction dérivable.
Et pour b) tu sais que tan(0) = 0 et l'intégrale une fonction sur un intervalle vide (i.e. Entre 0 et 0 par exemple est forcément nulle, toi qui est
Physicien, ça serait l'aire d'un segment ^^
par Mikihisa » 01 Aoû 2014, 21:44
Pour la fin de la question b) on te demande calculer u(0) car le calcul de primitive se fait toujours a une constante près, ici u(x) est donc ma primitive de u'(x) qui s'annule en 0.
par zzzzzzzzz » 01 Aoû 2014, 21:57
pour la b) , j'avais bien vu que u(0)=0 , mais de là , MONTRER u(x)=x ?????? C'est de la magie pour moi ... (Je dis ça parce que je n'ai toujours pas réussi a déduire u'(x) de la 1) ..)
par zzzzzzzzz » 01 Aoû 2014, 22:04
Mais u'(x)=f(x) non ? étant donné que tan(x) et x s'annulent toutes deux en 0
32 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :