Bah non, u(x) = F(tan x), on sais déjà que F est tan son dérivable,
Donc u'(x) = (tan x)'.F'(tan x), derive de la composé de deux fonction.
u'(x) = 1+(tan x)^2.f(tan x).
A partir de la tu devrais y voir plus claire pour u(x)=x.
Suites / Primitives. Niveau supposé TS
32 messages
- Page 2 sur 2 - 1, 2
par zzzzzzzzz » 01 Aoû 2014, 22:17
oooh c'est la dérivée d'une composée c'est ça ? Je l'avais jamais utilisée comme ça
par zzzzzzzzz » 01 Aoû 2014, 22:21
Bah oui tu l'as écrit ... Enfin je reconnais le cours théorique , mais je l'avais limité à l'usage que j'en avais dans les exos de bac , donc j'ai oublié le cours tel qu'il était , et j'ai pas pu l'appliquer par instinct de cette façon...
par Mikihisa » 01 Aoû 2014, 22:23
J'ai jamais appris une seule dérivé usuel au lycée, je suis tjs repasser par la dérive de la composer xD.
Et f(x) = F'(x) c'est a dire la dérive de la primitive de 1/(1+t^2), et la tout deviens plus claire.
Je vais dormir, bon courage pour la suite !
Et f(x) = F'(x) c'est a dire la dérive de la primitive de 1/(1+t^2), et la tout deviens plus claire.
Je vais dormir, bon courage pour la suite !
par paquito » 02 Aoû 2014, 09:51
bonjour,
Tu as
....^nx^{2n})
, c'est la somme de (n+1) termes (de 0 à n) d'une suite géométrique de premier terme 1 et de raison )
;
^n=(-1)^n(x^{2n}))
,
appliquons
......
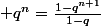; on obtient:
....^nx^{2n}=\frac{1-(-1)^{n+1}(x^2)^{n+1}}{1+x^2})
, mais
^{n+1}=-(-1)^n)
, donc le résultat devient:
....^nx^{2n}=\frac{1+(-1)^n(x^2)^{n+1}}{1+x^2})
^n(x^2))^{n+1}}{1+x^2})
où encore
....^nx^{2n}-\frac{1}{1+x^2}=\frac{(-1)^n(x^2)^{n+1}}{1+x^2})
Ensuite, on te demande d'établir une relation, pas de calculer toutes les intégrales; on intègre se 0 à 1:
....^nx^{2n})dx-\bigint_{0}^{1}(\frac{1}{1+x^2}dx=\bigint_{0}^{1}(\frac{(-1)^n(x^2)^{n+1}}{1+x^2})dx)
; or:
....+^nx^{2n})dx)
=
+.......^nx^{2n}dx)
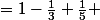......^n}{2n+1}=U_n)
.
Bon, j'ai tout détaillé; ça devrait aller; tu auras encore besoin de la dérivée de)
; c'est )
Tu as
appliquons
Ensuite, on te demande d'établir une relation, pas de calculer toutes les intégrales; on intègre se 0 à 1:
Bon, j'ai tout détaillé; ça devrait aller; tu auras encore besoin de la dérivée de
exo 2
par holycloud » 13 Aoû 2014, 22:18
Bonjour,
J'ai moi aussi ce devoirs a faire pendant les vacances, et même si je m en sort pas trop mal :lol3: ,
j'ai un peu de mal avec des questions de l'exercice 2:
La question 3)b) et la question 4)c) sont en train de me rendre fou :help:
Si quelqu'un peu me mettre sur la bonne piste pour l une ou l'autre de ces questions, merci a lui ou a elle.
Ps: le devoirs ce trouve la:
http://www.google.fr/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&ved=0CCgQFjAB&url=http%3A%2F%2Fwww.prepa-cpe.fr%2FIMG%2FUserFiles%2FFiles%2FRentr%25C3%25A9e%25202014%2FMath%2520-%2520Devoir%2520%25202014%2520Sup.pdf&ei=X9XrU_fyHMXmyQO0tILgDw&usg=AFQjCNEPxbabT_Mv1XFSZ8aTuzupoJ3BTw&sig2=CVnNh5IcuZMfIbmBKzPDJQ
J'ai moi aussi ce devoirs a faire pendant les vacances, et même si je m en sort pas trop mal :lol3: ,
j'ai un peu de mal avec des questions de l'exercice 2:
La question 3)b) et la question 4)c) sont en train de me rendre fou :help:
Si quelqu'un peu me mettre sur la bonne piste pour l une ou l'autre de ces questions, merci a lui ou a elle.
Ps: le devoirs ce trouve la:
http://www.google.fr/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&ved=0CCgQFjAB&url=http%3A%2F%2Fwww.prepa-cpe.fr%2FIMG%2FUserFiles%2FFiles%2FRentr%25C3%25A9e%25202014%2FMath%2520-%2520Devoir%2520%25202014%2520Sup.pdf&ei=X9XrU_fyHMXmyQO0tILgDw&usg=AFQjCNEPxbabT_Mv1XFSZ8aTuzupoJ3BTw&sig2=CVnNh5IcuZMfIbmBKzPDJQ
par paquito » 14 Aoû 2014, 08:40
3)b) dire que M appartient au cercle )
de centre A(-1) et de rayon 2 signifie que |z+1|=2 (AM=2); or on a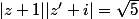 
, donc 
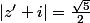, ce qui veut dire que M' appartient au cercle )
de centre C(-i) et de rayon 
4)c) On a:=(\hat{\vec{AM};\vec{BM}}))
et z' réel
imaginaire pur, soit =\frac{\pi}{2}+k\pi.)
On obtient:=\frac{\pi}{2}+k\p)
, ce qui caractérise le cercle de diamètre [AB] privé du point A .
Son centre a pour affixe
et son rayon vaut
4)c) On a:
On obtient:
Son centre a pour affixe
par lea_bloub » 01 Sep 2014, 11:37
Bonjour ! Désolé de vous déranger, je souhaiterais savoir dans le premier exercice, comment peut on trouver le n0 (question 2 du C)
Merci d'avance de votre aide
Merci d'avance de votre aide
par paquito » 02 Sep 2014, 11:30
lea_bloub a écrit:Oui je suis partie de la, mais Un-pi/4=O non ?
Tu as immédiatement |
32 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 110 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :