On donne
[CENTER]
On donne également la décomposition en éléments simples :
[CENTER]
1°) Je dois déterminer la constante
Pour cela, je cherche
Mais je me heurte à un problème :
Une idée de là où j'ai pu faire une faute ?
Merci d'avance :+++:
Variable aléatoire à densité
13 messages
- Page 1 sur 1
Variable aléatoire à densité
par capitaine nuggets » 01 Juin 2014, 20:28
Bonjour, je bloque sur un calcul d'intégrale généralisée.
On donne
la variable aléatoire réelle de densité :
[CENTER]= \frac{a}{x^2(x+1)} \mathbb{1}_{]1,+\infty[}(x))
.[/CENTER]
On donne également la décomposition en éléments simples :
[CENTER]}=\frac{1}{x^2}-\frac{1}{x}+\frac{1}{x+1})
.[/CENTER]
1°) Je dois déterminer la constante
de telle manière que 
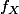
est effectivement bien une densité de .
Pour cela, je cherche tel que \ dx=1)
.
\ dx=\int_1^{+\infty} \frac{a}{x^2(x+1)}\ dx<br />=a \left( \int_1^{+\infty} \frac{1}{x^2}\ dx- \int_1^{+\infty} \frac{dx}{x}+\int_1^{+\infty} \frac{dx}{x+1} \right))
.
Mais je me heurte à un problème :
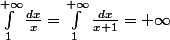
donc je ne vois pas comment continuer...
Une idée de là où j'ai pu faire une faute ?
Merci d'avance :+++:
On donne
[CENTER]
On donne également la décomposition en éléments simples :
[CENTER]
1°) Je dois déterminer la constante
Pour cela, je cherche
Mais je me heurte à un problème :
Une idée de là où j'ai pu faire une faute ?
Merci d'avance :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
par jlb » 01 Juin 2014, 21:25
avec les intégrales généralisées, Le Truc, c'est de faire tes calculs de 1 à t et tu regardes ensuite ce qui se passe qd t tend vers +infini.
A vérifier, je n'ai pas le temps mais les ln vont certainement donner une forme sympa en les regroupant.
Mais bon, je n'ai pas fait ls calculs, vérifie que cela va!!! bonne chance. { en regardant bien tu vas avoir ln(1+t)-lnt=ln(1+1/t)=...donc ça ira bien}
A vérifier, je n'ai pas le temps mais les ln vont certainement donner une forme sympa en les regroupant.
Mais bon, je n'ai pas fait ls calculs, vérifie que cela va!!! bonne chance. { en regardant bien tu vas avoir ln(1+t)-lnt=ln(1+1/t)=...donc ça ira bien}
par capitaine nuggets » 01 Juin 2014, 22:20
jlb a écrit:avec les intégrales généralisées, Le Truc, c'est de faire tes calculs de 1 à t et tu regardes ensuite ce qui se passe qd t tend vers +infini.
A vérifier, je n'ai pas le temps mais les ln vont certainement donner une forme sympa en les regroupant.
Mais bon, je n'ai pas fait ls calculs, vérifie que cela va!!! bonne chance. { en regardant bien tu vas avoir ln(1+t)-lnt=ln(1+1/t)=...donc ça ira bien}
A ok, merci, je vais voir ça ! :++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
par ARIMA » 05 Juil 2014, 18:36
Le truc c'est de ne pas séparer ton intégrale...
Tu peux faire le changement de variable u=1/x ce qui donne une intégrale qui se calcule facilement.
Tu peux faire le changement de variable u=1/x ce qui donne une intégrale qui se calcule facilement.
par adrien69 » 05 Juil 2014, 20:11
ARIMA a écrit:Le truc c'est de ne pas séparer ton intégrale...
Tu peux faire le changement de variable u=1/x ce qui donne une intégrale qui se calcule facilement.
Je ne suis pas vraiment de cet avis.
La méthode de jlb marche très bien. Et c'est la façon classique de faire quand on a des "intégrales téléscopiques" (j'utilise ce terme pour mettre en parallèle la méthode sur les séries, où l'on fait exactement pareil)
par ARIMA » 05 Juil 2014, 20:22
Quand est-ce que j'ai dit que ça ne marchait pas?
En quoi le changement de variable est une mauvaise idée?...
En quoi le changement de variable est une mauvaise idée?...
par adrien69 » 05 Juil 2014, 21:20
ARIMA a écrit:Quand est-ce que j'ai dit que ça ne marchait pas?
En quoi le changement de variable est une mauvaise idée?...
Quand tu as dit "le truc c'est de..." en mode réprobateur.
Le soucis de ton changement de variable, c'est que quand tu poses u=1/x dans dx/(1+x), eh bien ça fait n'importe quoi.
Sauf si je calcule mal de tête ou que je n'ai pas compris ce que tu voulais dire.
par ARIMA » 05 Juil 2014, 21:32
Tu vois un "mode" réprobateur dans une phrase tout à fait innocente, c'est un autre moyen de calcul que je proposais...
u=1/x => du = -dx/x^2
1/(x+1) => 1/(1/u+1) = u/(u+1) = 1 - 1/(1+u)
En intégrant sur [0,1] ça donne
1- ln(2), tout comme avec l'autre méthode.
u=1/x => du = -dx/x^2
1/(x+1) => 1/(1/u+1) = u/(u+1) = 1 - 1/(1+u)
En intégrant sur [0,1] ça donne
1- ln(2), tout comme avec l'autre méthode.
par adrien69 » 05 Juil 2014, 21:48
Saut que dans ce cas là tu es aussi obligé de faire une décomposition en élément simples, puis de te limiter à [t,1] et de faire tendre t vers 0.
On se retrouve avec la même méthode, plus une autre décomposition et un changement de variables.
On se retrouve avec la même méthode, plus une autre décomposition et un changement de variables.
par ARIMA » 05 Juil 2014, 21:52
Quelle décomposition en élément simple?
Passer de u/(u+1) à 1-1/(1+u) ?
C'est une évidence... u/(u+1) = (u+1-1)/(u+1)
C'est sur qu'à un moment donné il faudra faire des calculs ...
Me limiter à [t,1] et faire tendre vers 0? Pour quoi faire?
Si tu as décidé que tu avais raison et que ma méthode n'était pas bonne, je peux te donner raison, on gagnera du temps.
Passer de u/(u+1) à 1-1/(1+u) ?
C'est une évidence... u/(u+1) = (u+1-1)/(u+1)
C'est sur qu'à un moment donné il faudra faire des calculs ...
Me limiter à [t,1] et faire tendre vers 0? Pour quoi faire?
Si tu as décidé que tu avais raison et que ma méthode n'était pas bonne, je peux te donner raison, on gagnera du temps.
par adrien69 » 05 Juil 2014, 22:05
Je viens de tilter là où on avait mésentente.
Je pensais que tu reprenais de 1/(x+1)-1/x, auquel cas ça aurait été une perte de temps sans nom, mais non, tu repars du début. La question de nuggets m'a fait croire que ce n'était pas le cas.
Mea maxima culpa. En effet, ton truc marche et va plus vite. Et en effet, c'est même "l'astuce" classique.
Je pensais que tu reprenais de 1/(x+1)-1/x, auquel cas ça aurait été une perte de temps sans nom, mais non, tu repars du début. La question de nuggets m'a fait croire que ce n'était pas le cas.
Mea maxima culpa. En effet, ton truc marche et va plus vite. Et en effet, c'est même "l'astuce" classique.
par ARIMA » 05 Juil 2014, 22:06
Super, on est d'accord :)
Je déteste tout ce qui est en rapport avec les éléments simples, d'où mon idée de ne pas utiliser l'astuce proposée et d'en proposer une autre ;)
Je déteste tout ce qui est en rapport avec les éléments simples, d'où mon idée de ne pas utiliser l'astuce proposée et d'en proposer une autre ;)
par adrien69 » 05 Juil 2014, 22:08
De toute façon les éléments simples ça n'est qu'une façon de trouver une primitive, et donc in fine, un bon changement de variable.
Du coup si tu le vois directement, y a pas de raison de s'en priver.
Du coup si tu le vois directement, y a pas de raison de s'en priver.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :