[résolu]Démontrer un alignement

[Frednight]

Bonjour à tous

Dans la figure suivante, je souhaite démontrer l'alignement des points A', B' et P4 :


J'y suis bien parvenu de la façon suivante
On a :

Je pose :

On a alors :

et étant deux vecteurs non colinéaires, on en déduit que :

Et donc :


On obtient donc finalement que :

et


On a donc finalement donc les points A', B' et sont bien alignés.
Pas de problème dans cette démonstration de mon point de vue, si ce n'est qu'elle est un peu longue et je me demandais si vous auriez une démo plus courte à me proposer...?

Merci d'avance

[chan79]

Bonjour à tous

Dans la figure suivante, je souhaite démontrer l'alignement des points A', B' et P4 :

salut
Une méthode:
Je suppose que P1, P2, P3 et P4 sont régulièrement espacés.
Si on prend comme repère (P1,P2,A)
P1(0,0) P2(1,0) P3(2,0) P4(3,0) A(0,1)
On pose C(0,a) a réel
On trouve A'(0,2a-1)
Equation de (CP3): y=-a*x/2 + a
Equation de (AP2): y=-x+1
Ce qui donne pour l'intersection B des deux droites précédentes: B((2a-2)/(a-2),-a/(a-2))
C' étant le symétrique de C par rapport à B, on obtient C'((4a-4)/(a-2),-a²/(a-2))
B' étant le symétrique de B par rapport à C': B'((6a-6)/(a-2),(-2a²+a)/(a-2))



soit
On cherche les coordonnées de
La colinéarité de et de est facile à vérifier.
A', B' et P4 sont bien alignés

Reste à voir le cas a=2 (impossible)

[paquito]

Je pense aussi qu'il doit y avoir plus court, mais je ne vois pas P4 et je ne sais comment P1, P2 et P4 sont définis; par contre, tu as une magifique configuration de médianes dans le triangle AA'B'; je ne sais pas si on peut l'exploiter.

[Frednight]

Je pense aussi qu'il doit y avoir plus court, mais je ne vois pas P4 et je ne sais comment P1, P2 et P4 sont définis

, , et sont alignés et
J'ai essayé de modifier mon image pour qu'elle rentre dans les dimensions standards du forum mais est-ce que vous sauriez comment modifier l'échelle d'affichage des images sur le forum?

par contre, tu as une magifique configuration de médianes dans le triangle AA'B'; je ne sais pas si on peut l'exploiter.

Oui je l'ai démontrée précédemment et je m'en suis servi dans mes décompositions vectorielles mais je ne sais pas s'il y a moyen de s'en servir plus simplement pour démontrer ce que je cherche

Une méthode:
Je suppose que P1, P2, P3 et P4 sont régulièrement espacés.
Si on prend comme repère (P1,P2,A)
P1(0,0) P2(1,0) P3(2,0) P4(3,0) A(0,1)
On pose C(0,a) a réel
On trouve A'(0,2a-1)
Equation de (CP3): y=-a*x/2 + a
Equation de (AP2): y=-x+1
Ce qui donne pour l'intersection B des deux droites précédentes: B((2a-2)/(a-2),-a/(a-2))
C' étant le symétrique de C par rapport à B, on obtient C'((4a-4)/(a-2),-a²/(a-2))
B' étant le symétrique de B par rapport à C': B'((6a-6)/(a-2),(-2a²+a)/(a-2))



soit
On cherche les coordonnées de
La colinéarité de et de est facile à vérifier.
A', B' et P4 sont bien alignés

Reste à voir le cas a=2 (impossible)

Merci encore une fois pour ton aide Chan :we:

[paquito]

J'ai un peu regardé ta figure sur géogébra, on a l'alignement quand tout est bien respecté, ce qui veut dire qu'il ne faut pas négliger une hypothèse et qu'il faut à un moment donné, les utiliser; donc pas de démonstration éclair.
mais ta démonstration est très bien et tu as celle de chan si tu préfères le calculs.
Bonnes vacances.

[Frednight]

J'ai un peu regardé ta figure sur géogébra, on a l'alignement quand tout est bien respecté, ce qui veut dire qu'il ne faut pas négliger une hypothèse et qu'il faut à un moment donné, les utiliser; donc pas de démonstration éclair.
mais ta démonstration est très bien et tu as celle de chan si tu préfères le calculs.
Bonnes vacances.

Je suppose qu'il doit quand même y avoir une façon rapide de le démontrer en passant par des projecteurs mais effectivement, avec les outils standards du lycée les démonstrations doivent sans doute se limiter à ce que l'on a déjà fait

[Ben314]

Salut,
A mon avis, si on doit travailler dans un repère, me semble plus simple :

est le milieu de donc et il est sur d'équation donc .
d'où et donc

[paquito]

Je suppose qu'il doit quand même y avoir une façon rapide de le démontrer en passant par des projecteurs mais effectivement, avec les outils standards du lycée les démonstrations doivent sans doute se limiter à ce que l'on a déjà fait

Pour utiliser des projecteurs, il faudrait des droites parallèles, ce qui n'est pas le cas. Si chan n'a pas trouvé de méthode élégante, à mon avis, il n'y en a pas! Je viens de regarder la dernière version de chan; à mon avis il optimise la situation et je crois que c'est cette démonstration analytique qui est la plus performante.

[Ben314]

Si on veut éviter les repères/calculs vectoriels, on peut utiliser à la place des compositions d'homothéties.
C'est plus joli mais ça demande un peu d'astuce pour savoir comment les composer de façon maline.

Et là, comme la preuve avec un repère tient 2 ligne, je sais pas si ça vaut le coup de se fouler...

[Ben314]

Une preuve avec les homothéties (et hélas un peu de calcul vectoriel...)

Soient et les réels tels que .
Comme la composée de ces deux homothétie est centrée en un point de et qu'elle envoie sur , c'est l'homothétie de centre et de rapport donc .

De on déduit que
De on déduit que

Donc .
Comme la composée de ces deux homothétie est centrée en un point de et qu'elle envoie sur , c'est l'homothétie de centre l'intersection de et de et de rapport .
De on déduit que

[Frednight]

Et là, comme la preuve avec un repère tient 2 ligne, je sais pas si ça vaut le coup de se fouler...

Tes deux preuves sont impeccables. Merci beau coup pour ton aide

[paquito]

Tu as l'air de bien aimer la géométrie et de regretter les raisonnements géométriques et l'utilisation des transformation (symétries, homothéties, rotations) au profit de l'analytique qui rend les démonstrations fades et longues. je te propose un grand classique traité à l'ancienne.

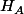
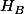
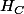
ABC est un triangle quelconque, on note I,J et K les milieux de[BC], [AC] et [AB] , O le centre du cercle circonscrit à ABC noté , G son centre de gravité et , et les pieds des hauteurs.

1) Soit h l'homothétie de centre G et de rapport -2;
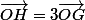
Quelle est l'image de I Par h? de (OI)? En déduire que les 3 hauteurs sont concourantes en H=h(O) et que G, H, et O sont alignés avec . ces 3 points défiinissent une droite qui est la droite d'Euler du triangle.

2) Soit A' le point diamétralement opposé à A sur et K le symétrique de A' par rapport à I. Quelle est la nature de BA'CK. Montrer que (BK) et (CK) sont 2 hauteurs et que K=H.

3) On appelle G le symétrique orthogonal de H par rapport à (BC); démontrer que AA'G est rectangle en G (on pourra s'aider du triangle A'GH ) et en déduire que G est sur ;
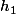
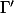
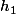
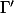
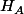
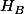
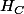
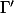
soit l'homothétie de centre H et de rapport 1/2; on note le cercle image de par . déduire de ce qui précède que contient les points I,J,K, , , et les milieux des segments [AH], [BH] et [CH]; préciser la position de son centre. ( est le cercle des 9 points du triangle ABC.

Je n'ose pas imaginer une démonstration analytique!

[Ben314]

Je viens de trouver une autre preuve (que je trouve plus jolie : bien plus générale et quasi pas de calcul)


Pour une meilleure compréhension j'ai renommé les points, donné deux noms au même point et introduit le point (symétrique de par rapport à )

Si, pour tout réel , on pose , alors, par construction, les 3 points sont alignés, ainsi que les 3 points et les 3 points .
Or les points sont alignés ssi est nul (déterminant calculé dans une base quelconque)
Sauf que est clairement un polynôme de degré au plus 2 et qu'on vient de voir que les trois réels , et sont racines de .
Le polynôme est donc identiquement nul ce qui signifie que, quelque soit le réel , les points sont alignés et, en particulier, sont alignés.

[paquito]

Je viens de trouver une autre preuve (que je trouve plus jolie : bien plus générale et quasi pas de calcul)


Pour une meilleure compréhension j'ai renommé les points, donné deux noms au même point et introduit le point (symétrique de par rapport à )

Si, pour tout réel , on pose , alors, par construction, les 3 points sont alignés, ainsi que les 3 points et les 3 points .
Or les points sont alignés ssi est nul (déterminant calculé dans une base quelconque)
Sauf que est clairement un polynôme de degré au plus 2 et qu'on vient de voir que les trois réels , et sont racines de .
Le polynôme est donc identiquement nul ce qui signifie que, quelque soit le réel , les points sont alignés et, en particulier, sont alignés.

Très joli! Bravo chan!

[chan79]

Très joli! Bravo chan!

Merci, mais c'est Ben314 qu'il faut féliciter ... :ptdr:

[paquito]

Merci, mais c'est Ben314 qu'il faut féliciter ... :ptdr:

On peut vous féliciter tous les deux! :id:

[zygomatique]

salut

en regardant plus ou moins et voyant des homothéties il me semble qu'une autre méthode (vectorielle certes mais qui permet de se débarrasser de beaucoup de calculs analytique) est le calcul barycentrique puisque dire que trois points sont alignés équivaut à dire que l'un est le barycentre des deux autres ...

et j'en vois plein de barycentres ....

P4 = bar{(P1, 1), (P3, -3)}

P1 = bar{(A', 2), (C, -1)}

P3 = bar{(B', 4), (C, -1)}

puis associativité du barycentre ... bla bla bla

ici ça ne marche pas j'ai supposé d'après la figure que A' est le milieu de [CP1] ce qui ne semble pas le cas au vu des figures suivantes ....

peut-être un énoncé complet ? ....

ha mais si il me semble ::

donc P4 = bar{(A', 2), (C, -1), (B', -4) , (C, 1)} = bar{(A', 2), (B', -4)}

ce qui signifie que B' est le milieu de [A', P4] ... mais ça ne semble pas au vu des figure de ben314

énoncé à confirmer et dans le meilleur des cas 5 lignes de français suffisent sans aucun calcul :lol3:

[Ben314]

Enoncé "complet"
Soit 4 points alignés (dans cet ordre) et équidistants, un point extérieur à cette droite, un point de , l'intersection de et , le symétrique de par rapport à et enfin le point tel que

Montrer que , et sont alignés.

ça peut évidement se faire avec des barycentre vu qu'entre barycentres et repères, c'est à peu prés la même chose : par exemple la preuve utilisant le repère s'écrit de façon quasiment identique en terme de barycentres.

[zygomatique]

merci ... :lol3:

[Ben314]

Sinon, s'il y en a qui veulent "plus" :
Montrer que les 5 droites du dessin sont 5 tangentes d'une même parabole.