Une simple suite...

[Ben314]

On fixe un entier naturel non nul et on définit la suite par :
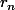
et où est le reste de la division euclidienne de par

1) Montrer que la suite est périodique,
c'est à dire qu'il existe tel que

2) Soit la plus petite période. Évaluer la somme

P.S. : Un tableur peut être utile pour... faire des conjectures que l'on démontrera ensuite...

[Doraki]

Bon pour l'instant j'arrive à montrer que un est toujours un entier entre 1 et a, et donc que la suite est éventuellement périodique de période p <= a².

On peut reformuler la relation de recurrence en la propriété que
un+2 est le plus grand entier <= a tel que un + un+2 soit un multiple de un+1.

Aussi, on a toujours un+un+1 > a, donc la relation de récurrence est aussi valable dans l'autre sens :
un est le plus grand entier <= a tel que un + un+2 soit un multiple de un+1.

Donc la suite est vraiment périodique.

J'ai essayé avec a=10 et la somme vaut ... 1 !

[jlb]

moi, j'ai tout réussi quand a=1 :ptdr:

[jlb]

moi, j'ai tout réussi quand a=1 :ptdr:

( sinon, dans le cas général, question 2, c'est du "télescopage"?)

[Doraki]

Lorsqu'on part en arrière, on obtient une symétrie autour du u1 = 1.
En outre, à moins que a soit égal à 1, au milieu de la période on a un autre truc du genre ... x y x ... (on peut pas avoir ... x x ... sans que toute la suite soit égale à x)
Donc p est pair et la suite des 1/un*un+1 a aussi une symétrie (du type ... x x ... y y ... cette fois).

Comme couples de valeurs consécutives on ne peut avoir que des couples (x,y) avec x+y > a et x premier avec a.
Si ça se trouve on obtient toujours tous les couples possibles dans la suite.
On pourrait alors montrer par récurrence sur a que la somme vaut bien 1.

Pour passer de a à a+1, on enlève de la somme tous les 1/xy avec x+y = a+1 et x et y premiers entre eux; et on rajoute tous les 1/x(a+1) et les 1/(a+1)x pour 1 <= k <= a premier avec a+1.
Comme 1/xy = 1/x(x+y) + 1/(x+y)y, ça m'a l'air de bien se goupiller.

[Ben314]

Comme couples de valeurs consécutives on ne peut avoir que des couples (x,y) avec x+y > a et x premier avec a.
Si ça se trouve on obtient toujours tous les couples possibles dans la suite....

J'ai effectivement failli mettre comme question "donner une c.n.s. sur (c,d) pour qu'il existe n tel que un=c et u(n+1)=d...

[Doraki]

En fait, on montre ça aussi par récurrence une fois qu'on voit que pour obtenir la suite pour a, on prend la suite pour a-1 et on insère des "a" entre chaque couple de valeurs consécutives (x,y) avec x+y=a.
Du coup l'argument 1/xy = 1/x(x+y) + 1/(x+y)y montre que la somme est inchangée.

[Ben314]

En fait, on montre ça aussi par récurrence une fois qu'on voit que pour obtenir la suite pour a, on prend la suite pour a-1 et on insère des "a" entre chaque couple de valeurs consécutives (x,y) avec x+y=a.
Du coup l'argument 1/xy = 1/x(x+y) + 1/(x+y)y montre que la somme est inchangée.

Oui,ça roule... :++:

Tu arrive à montrer proprement que la suite partant de a s'obtient en partant de la suite précédente et en intercalant des a entre les x<y t.q. x+y=a ?

[Ben314]

Si il y en a que ça interesse, en fait la suite en question, c'est la suite des dénominateurs de la a-ième suite de Faray, et, pour n'importe quel , la somme de k=0 à n-1 des 1/(uku(k+1)) c'est le n-ième terme de la suite de Faray.

[jlb]

Salut, je fais une erreur où pour a différent de 1, u2=a-1,u3=a-2,....u(a-1)=2,u(a)=1 et u(a+1)=a


puis la somme demandée s'obtient facilement par télescopage en utilisant 1/(k(k-1))=1/(k-1)-1/k?