Tribu borélienne
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jujudu597
- Membre Naturel
- Messages: 87
- Enregistré le: 20 Fév 2014, 17:13
-
 par jujudu597 » 01 Avr 2014, 10:24
par jujudu597 » 01 Avr 2014, 10:24
Bonjour,
Comment puis je montrer que Bor(
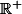
)
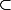
Bor(

)
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 01 Avr 2014, 10:51
par mrif » 01 Avr 2014, 10:51
jujudu597 a écrit:Bonjour,
Comment puis je montrer que Bor(
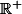
)
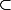
Bor(

)
Tu utilises tout simplement la définition de la tribu borélienne, à savoir la tribu engendrée par la famille des ouverts.
Soit

la famille des ouverts de

.
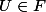
ssi il existe

ouvert de

tq
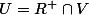
.

et

sont des éléments de
)
, donc
)
, ce qui montre que
)
.
Il te reste à conclure en utilisant ton cours.
-
jujudu597
- Membre Naturel
- Messages: 87
- Enregistré le: 20 Fév 2014, 17:13
-
 par jujudu597 » 01 Avr 2014, 13:16
par jujudu597 » 01 Avr 2014, 13:16
mrif a écrit:Tu utilises tout simplement la définition de la tribu borélienne, à savoir la tribu engendrée par la famille des ouverts.
Soit

la famille des ouverts de

.
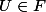
ssi il existe

ouvert de

tq
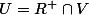
.

et

sont des éléments de
)
, donc
)
, ce qui montre que
)
.
Il te reste à conclure en utilisant ton cours.
ah mercii!
Je pense avoir compris.
Pour la fin, c'est juste
)
. Donc
 \subset Bor(\mathbb{R}))
donc comme
 = bor (R^+))
... CQFD
-
jujudu597
- Membre Naturel
- Messages: 87
- Enregistré le: 20 Fév 2014, 17:13
-
 par jujudu597 » 01 Avr 2014, 13:45
par jujudu597 » 01 Avr 2014, 13:45
Et maintenant, si
)
, comment montrer que
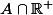
)
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 01 Avr 2014, 13:45
par mrif » 01 Avr 2014, 13:45
jujudu597 a écrit:ah mercii!
Je pense avoir compris.
Pour la fin, c'est juste
)
. Donc
 \subset Bor(\mathbb{R}))
donc comme
 = bor (R^+))
... CQFD
Oui c'est ça à une erreur de frappe près:
.............comme
 = bor (R^+))
-
jujudu597
- Membre Naturel
- Messages: 87
- Enregistré le: 20 Fév 2014, 17:13
-
 par jujudu597 » 01 Avr 2014, 13:55
par jujudu597 » 01 Avr 2014, 13:55
mrif a écrit:Oui c'est ça à une erreur de frappe près:
.............comme
 = bor (R^+))
Ah oui merci
Et pour si A
)
, comment montrer que
)
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 01 Avr 2014, 14:39
par mrif » 01 Avr 2014, 14:39
jujudu597 a écrit:Ah oui merci
Et pour si A
)
, comment montrer que
)
Tu considère l'ensemble
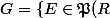\ \|\ E \cap R^+ \in Bor(R^+) \})
Tu montres que

est une tribu sur

qui contient tous les ouverts de

donc elle contient
)
et tu conclues.
Remarque: cette méthode a été maintes fois utilisée dans ton cours pour différentes démonstrations, autrement ce serait difficile à trouver.
-
jujudu597
- Membre Naturel
- Messages: 87
- Enregistré le: 20 Fév 2014, 17:13
-
 par jujudu597 » 01 Avr 2014, 15:16
par jujudu597 » 01 Avr 2014, 15:16
mrif a écrit:Tu considère l'ensemble
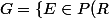\ \|\ E \cap R^+ \in Bor(R^+) \})
Tu montres que

est une tribu sur

qui contient tous les ouverts de

donc elle contient
)
et tu conclues.
Remarque: cette méthode a été maintes fois utilisée dans ton cours pour différentes démonstrations, autrement ce serait difficile à trouver.
Ca me semble si compliqué

COmment montrer que si
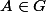
alors
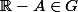
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 01 Avr 2014, 15:44
par mrif » 01 Avr 2014, 15:44
jujudu597 a écrit:Ca me semble si compliqué

COmment montrer que si
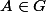
alors
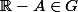
Il peut y avoir plus simple mais je n'en vois pas.
)
, son complémentaire dans

est
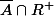
qui appartient à
)
, donc
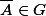
-
jujudu597
- Membre Naturel
- Messages: 87
- Enregistré le: 20 Fév 2014, 17:13
-
 par jujudu597 » 01 Avr 2014, 15:49
par jujudu597 » 01 Avr 2014, 15:49
mrif a écrit:Il peut y avoir plus simple mais je n'en vois pas.
)
, son complémentaire dans

est
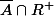
qui appartient à
)
, donc
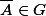
Vous dites que
^c = A^c \in R^+)
??
Si c'est ca je ne vois pas pourquoi
-
jujudu597
- Membre Naturel
- Messages: 87
- Enregistré le: 20 Fév 2014, 17:13
-
 par jujudu597 » 02 Avr 2014, 11:05
par jujudu597 » 02 Avr 2014, 11:05
mrif a écrit:Il peut y avoir plus simple mais je n'en vois pas.
)
, son complémentaire dans

est
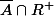
qui appartient à
)
, donc
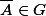
Mais on ne pas dire simplement que A s'écrit comme union dénombrable d'intervalle ouvert de R?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Avr 2014, 11:08
par Ben314 » 02 Avr 2014, 11:08
[0,1] (fermé) c'est un borélien de R ?
Tu peut l'écrire comme réunion dénombrables d'intervalles ouverts de R ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
jujudu597
- Membre Naturel
- Messages: 87
- Enregistré le: 20 Fév 2014, 17:13
-
 par jujudu597 » 02 Avr 2014, 13:27
par jujudu597 » 02 Avr 2014, 13:27
Ben314 a écrit:[0,1] (fermé) c'est un borélien de R ?
Tu peut l'écrire comme réunion dénombrables d'intervalles ouverts de R ?
Non mais son complémentaire oui

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Avr 2014, 15:08
par Ben314 » 02 Avr 2014, 15:08
jujudu597 a écrit:Non mais son complémentaire oui
Peut être, mais ça signifie quand même que la réponse à ta question
jujudu597 a écrit:Mais on ne pas dire simplement que A s'écrit comme union dénombrable d'intervalle ouvert de R?
est
non...

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
jujudu597
- Membre Naturel
- Messages: 87
- Enregistré le: 20 Fév 2014, 17:13
-
 par jujudu597 » 02 Avr 2014, 15:25
par jujudu597 » 02 Avr 2014, 15:25
Ben314 a écrit:Peut être, mais ça signifie quand même que la réponse à ta questionest
non...

xD Je suis perdu!
-
jujudu597
- Membre Naturel
- Messages: 87
- Enregistré le: 20 Fév 2014, 17:13
-
 par jujudu597 » 02 Avr 2014, 15:40
par jujudu597 » 02 Avr 2014, 15:40
Ma question de base est si j'ai une fonction
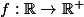
,
est t'il équivalent de dire que f est mesurable
 - Bor(\mathbb{R}))
et que f est mesurable
 - Bor(\mathbb{R}^+))

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Avr 2014, 15:48
par Ben314 » 02 Avr 2014, 15:48
jujudu597 a écrit:Ma question de base est si j'ai une fonction
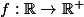
,
est t'il équivalent de dire que f est mesurable
 - Bor(\mathbb{R}))
et que f est mesurable
 - Bor(\mathbb{R}^+))
Tu as la réponse juste au dessus (donnée par mrif) : vu que les borélien de R+, c'est les traces sur R+ des boréliens de R, ben c'est texto la même chose d'être "mesurable
 -> Bor(\mathbb{R}))
" et "mesurable
 -> Bor(\mathbb{R}_+))
(et heureusement...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
jujudu597
- Membre Naturel
- Messages: 87
- Enregistré le: 20 Fév 2014, 17:13
-
 par jujudu597 » 02 Avr 2014, 15:54
par jujudu597 » 02 Avr 2014, 15:54
Ben314 a écrit:Tu as la réponse juste au dessus (donnée par mrif) : vu que les borélien de R+, c'est les traces sur R+ des boréliens de R, ben c'est texto la même chose d'être "mesurable
 -> Bor(\mathbb{R}))
" et "mesurable
 -> Bor(\mathbb{R}_+))
(et heureusement...)
les traces?
-
jujudu597
- Membre Naturel
- Messages: 87
- Enregistré le: 20 Fév 2014, 17:13
-
 par jujudu597 » 02 Avr 2014, 16:17
par jujudu597 » 02 Avr 2014, 16:17
Aussi par rapport à la réponse de mrif,
)
, son complémentaire dans

est
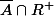
qui appartient à
)
, donc
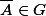
Je ne vois pas pourquoi on prend le complémentaire dans

, pour moi ca devrait etre le complémentaire dans R

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Avr 2014, 16:44
par Ben314 » 02 Avr 2014, 16:44
jujudu597 a écrit:les traces?
Quand on considère les intersections de tas d'ensemble sur un ensemble fixé A, on appelle souvent ça la "trace sur A" des ensembles en question (c'est ce qu'il en reste lorsqu'on ne regarde que l'intersection avec A)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
)
Bor(
)
la famille des ouverts de
.
ssi il existe
ouvert de
tq
.
et
sont des éléments de
, donc
, ce qui montre que
.
, comment montrer que
est une tribu sur
qui contient tous les ouverts de
donc elle contient
et tu conclues.
,
et que f est mesurable
