Tribu Borélienne

[Robot]

Mais est-ce que ce que j'avais écrit est licite ?

A quoi fais-tu référence ?

[Ncdk]

A quoi fais-tu référence ?

Je fais référence à ma dernière réponse qui était :

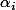
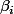
Donc en fait je peux tout simplement prendre un pavé quelconque disons x...x tel que et bien entendu , pas contre je me demandais s'il était impératif de dire que mes et sont dans ?

Je me disais que oui en fait car en faisant ça, comme on sait que est dense dans on pouvait dire que est une union au plus dénombrable car a ses éléments dans non ?

[Robot]

Ca ne va pas.
Des détails : est incorrect ( n'est pas un élément de )
a ses éléments dans : comment un pavé ouvert pourrait-il avoir tous ses éléments rationnels ? Ca nierait la densité.

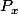
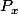
Mettons que tu aies voulu écrire qu'on prend pour tout dans à coordonnées rationnelles un pavé contenant et contenu dans . Mezalor rien ne dit que la réunion des est .

[Ncdk]

Ca ne va pas.
Des détails : est incorrect ( n'est pas un élément de )
a ses éléments dans : comment un pavé ouvert pourrait-il avoir tous ses éléments rationnels ? Ca nierait la densité.

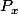
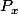
Mettons que tu aies voulu écrire qu'on prend pour tout dans à coordonnées rationnelles un pavé contenant et contenu dans . Mezalor rien ne dit que la réunion des est .

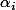
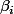
Mais prendre les et dans c'est correct non ?

[Robot]

Si on considère la collection de tous les pavés ouverts rationnels contenus dans U, ça va.

[Ncdk]

Si on considère la collection de tous les pavés ouverts rationnels contenus dans U, ça va.

D'accord merci pour ta réponse