Partie entière et suite arithmétique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 28 Mar 2014, 16:16
par t.itou29 » 28 Mar 2014, 16:16
Bonjour,
J'ai résolu ce problème (encore je suis même sur que ma solution soit correcte!) mais je suis persuadé qu'il y a une solution beaucoup plus simple et courte que je ne parviens pas à trouver :mur:
Voici le problème:
Si
_{n\ge1})
est une suite arithmétique alors a est un entier. ([x]=partie entière).
Et ma solution:
Supposons a non entier et écrivons-le a=m+h avec m un entier et

On a alors
(m+h)]-[n(m+h)]=m+[(n+1)h]-[nh])
Pour que la suite soit arithmétique il doit exister c tel que pour tout n non nul:
h]-[nh]=c)
et il est clair que c doit être un entier non nul.
En sommant l'égalité pour n allant de 1 à k on obtient:
h]=kc)
Or
h \ge [(k+1)h])
ce qui entraîne
\le h)
.
Or comme c>h pour k suffisamment grand l'inégalité n'est pas vérifiée. Contradiction.
Avez-vous des idées ?
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 28 Mar 2014, 16:27
par Monsieur23 » 28 Mar 2014, 16:27
Aloha,
Comme tu le dis, la raison c de la suite est nécessairement entière. On a donc pour tout n
[an] = cn, d'où [an]/n = c.
Or on sait que [an]/n = [a], d'où c=[a]. Finalement, pour tout n, [an] = [a]n. Et ceci n'est vrai que si a est entier (petit exercice sur les parties entières : dans l'idée, sinon la partie fractionnaire de a, multipliée par un n assez grand "ajoute 1" à la partie entière).
Mais ça ressemble pas mal à ce que tu as fait.
« Je ne suis pas un numéro, je suis un homme libre ! »
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 28 Mar 2014, 16:42
par t.itou29 » 28 Mar 2014, 16:42
Monsieur23 a écrit:Aloha,
Comme tu le dis, la raison c de la suite est nécessairement entière. On a donc pour tout n
[an] = cn, d'où [an]/n = c.
Or on sait que [an]/n = [a], d'où c=[a]. Finalement, pour tout n, [an] = [a]n. Et ceci n'est vrai que si a est entier (petit exercice sur les parties entières : dans l'idée, sinon la partie fractionnaire de a, multipliée par un n assez grand "ajoute 1" à la partie entière).
Mais ça ressemble pas mal à ce que tu as fait.
Comme le premier terme de la suite est [a] c'est pas plutôt [an]=nc+[a] ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Mar 2014, 16:57
par Ben314 » 28 Mar 2014, 16:57
Salut,
Ton hypothèse te dit que
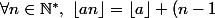r)
où

est la raison de la suite (évidement entier vu que c'est la différence entre deux termes successifs entiers de la suite).
Par définition de la partie entière, ça signifie que
r\leq an<\lfloor a \rfloor +(n-1)r +1)
et donc que

Si on fait tendre

vers l'infini, on en déduit que

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 28 Mar 2014, 17:04
par t.itou29 » 28 Mar 2014, 17:04
Ben314 a écrit:Salut,
Ton hypothèse te dit que
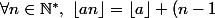r)
où

est la raison de la suite (évidement entier vu que c'est la différence entre deux termes successifs entiers de la suite).
Par définition de la partie entière, ça signifie que
r\leq an<\lfloor a \rfloor +(n-1)r +1)
et donc que

Si on fait tendre

vers l'infini, on en déduit que

D'accord j'ai compris, c'est plus simple comme ça ! Merci
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 28 Mar 2014, 22:13
par Monsieur23 » 28 Mar 2014, 22:13
t.itou29 a écrit:Comme le premier terme de la suite est [a] c'est pas plutôt [an]=nc+[a] ?
Ouais. J'avais pas vu le n>0

« Je ne suis pas un numéro, je suis un homme libre ! »
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
