IPP avec la divergence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
par LevinAnderson » 15 Fév 2014, 16:29
Bonjour à tous,
Je n'arrive pas à retrouver une formule qu'on a utilisé en cours, alors je fais appel à votre aide
Voilà ce qu'il y a à démontrer :
v dx = -\int_{\Omega}K\nabla u \cdot \nabla v dx + \int_{\partial \Omega}K\nabla u \cdot n v d\sigma)
avec
)
et
)
J'ai essayé de démontrer l'égalité en décomposant la divergence comme la somme des dérivées partielles de la fonction mais je bloque après !
Merci d'avance pour votre aide
-
DamX
- Membre Rationnel
- Messages: 630
- Enregistré le: 02 Oct 2012, 13:12
-
par DamX » 17 Fév 2014, 18:49
LevinAnderson a écrit:Bonjour à tous,
Je n'arrive pas à retrouver une formule qu'on a utilisé en cours, alors je fais appel à votre aide
Voilà ce qu'il y a à démontrer :
avec
et
J'ai essayé de démontrer l'égalité en décomposant la divergence comme la somme des dérivées partielles de la fonction mais je bloque après !
Merci d'avance pour votre aide
Bonjour,
C'est Green-Ostrogradsky, combiné aux règles de comportement du div sur un produit qui fait tomber le résultat :
on a :
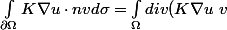 dx)
par Green-Ostrogradsky, et le terme de divergence dans le membre de droite se décompose un peu à la manière d'une dérivée d'un produit de fonctions pour donner le résultat voulu. (c'est la 8e ligne de
http://fr.wikipedia.org/wiki/Identit%C3%A9s_vectorielles, divergence du produit entre une fonction scalaire par une fonction vectorielle)
Damien
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
