FunkyAnts a écrit:Le dvl d'ordre n de la fonction f pour x qui tend vers l'infini donne une approximation de plus en plus précise de la fonction.
Oui : c'est évidement du "blabla", mais je sais pas trop ce qu'il faut répondre façe à une question du style "Que peut-on dire de..."
FunkyAnts a écrit:F admet un DLn en l'infini si et seulement si f(x)*(1/x) est dérivable en 0..
Non : "être dérivable" est équivalent à "admettre un D.L. à l'ordre 1" mais ça ne marche pas pour les D.L. à l'odre >1.
Ici, le seul truc que je vois à dire, c'est que l'on peut effectuer la division de
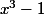
par

à l'ordre qu'on veut donc le D.L. à l'ordre n existze quelque soit n.
Mais si on veut écrire le D.L. à l'ordre n avec n quelconque, il faut un peut "tripoter" l'expression de F car on ne connait pas directement l'expression du D.L. de

.
Un truc qui peut venir à l'esprit, c'est de décomposer en éléments simples :
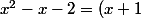(x-2))
donc

où

et

sont deux constantes réelles à determiner.
Cela permet d'avoir le D.L. à l'ordre qu'un veut vue que, lorsque
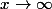
, on a

donc
^2+\big( \frac{ \lambda}{ x }\big)^3+\dots+\big( \frac{ \lambda}{ x }\big)^n+ o\big(\frac{1}{x^n}\big)\Big))
