Pourquoi Lim p*ln p =0, quand p tend vers 0?

[IdC]

Bonjour tout le monde :happy2:

j'ai à démonter pourquoi Lim p*ln p =0, quand p tend vers 0?

quelqu'un pour m'aider?

Merci d'avance :happy2:

[IdC]

re salut,

je viens de trouver la solution :we:

p*lnp=ln (p^p), or 0^0=1 donc ln(1)=0;

Merci quand même.

[girdav]

Comment justifies-tu le fait que ?

[IdC]

Comment justifies-tu le fait que ?

quelque soit x réel: x^0=1 :++:

[Nightmare]

Salut,

ln(x) < x

[Skullkid]

quelque soit x réel: x^0=1 :++:

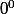
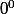
Je ne suis pas sûr que tu saches le démontrer pour ... La valeur de est une convention. On la fixe généralement à 1 car c'est cette valeur qui permet de généraliser le plus grand nombre de formules faisant intervenir des puissances. Mais on aurait tout aussi bien pu dire que , par exemple pour rendre continue la fonction en 0 (laquelle nécessite déjà une définition particulière quand x est irrationnel).

[gigamesh]

bonjour,
la démonstration classique utilise le fait que ln(x)/x tend vers zéro en l'infini.

commence par étudier la fonction ln(x)/racine(x) ; ensuite déduis-en la limite de ln(x)/x en l'infini.

Pour finir, pose p=1/x et utilise le théorème sur la limite d'une fonction composée.