Une somme...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 18 Aoû 2005, 16:51
par Anonyme » 18 Aoû 2005, 16:51
Bonjour,
je n'arrive pas à faire la somme de k=1 à n de (k-2) parmi (n-2)
peut etre faut il utiliser la formule du binôme de Newton ou se servi des propriétés du triangle de Pascal....
Enfin en tous cas merci à ceux qui se pencheront sur cette question.
-
N_comme_Nul
- Membre Relatif
- Messages: 127
- Enregistré le: 06 Aoû 2005, 22:00
-
 par N_comme_Nul » 18 Aoû 2005, 17:53
par N_comme_Nul » 18 Aoû 2005, 17:53
Salut !
Prenons

, que vaut :
)
?
-
Anonyme
 par Anonyme » 18 Aoû 2005, 17:59
par Anonyme » 18 Aoû 2005, 17:59
je ne suis pas sur qu'il attendait ce type de réponse.
-
N_comme_Nul
- Membre Relatif
- Messages: 127
- Enregistré le: 06 Aoû 2005, 22:00
-
 par N_comme_Nul » 18 Aoû 2005, 18:18
par N_comme_Nul » 18 Aoû 2005, 18:18
Salut !
La remarque que j'ai faite, est je pense, importante. Quel sens donner à "-1 parmi -1" ? D'ailleurs, le premier terme de la somme proposée est toujours "-1 par mi n-2" quel que soit n.
-
gamecuber
- Membre Naturel
- Messages: 36
- Enregistré le: 01 Mai 2005, 01:14
-
 par gamecuber » 18 Aoû 2005, 18:26
par gamecuber » 18 Aoû 2005, 18:26
"N_comme_Nul" a écrit:Quel sens donner à "-1 parmi -1" ? D'ailleurs, le premier terme de la somme proposée est toujours "-1 par mi n-2" quel que soit n.
Par définition, ça vaut 0 (cf. :
http://fr.wikipedia.org/wiki/Coefficient_binomial), donc la notation de Razor est correcte.
-
N_comme_Nul
- Membre Relatif
- Messages: 127
- Enregistré le: 06 Aoû 2005, 22:00
-
 par N_comme_Nul » 18 Aoû 2005, 18:29
par N_comme_Nul » 18 Aoû 2005, 18:29
Salut !
Encore faudrait-il que -1 soit un entier naturel :triste:
-
gamecuber
- Membre Naturel
- Messages: 36
- Enregistré le: 01 Mai 2005, 01:14
-
 par gamecuber » 18 Aoû 2005, 18:30
par gamecuber » 18 Aoû 2005, 18:30
On a somme de k=1 à n de C(n-2,k-2)=somme de i=0 à n-2 de C(n-2,i) = 2^(n-2)
a+
-
gamecuber
- Membre Naturel
- Messages: 36
- Enregistré le: 01 Mai 2005, 01:14
-
 par gamecuber » 18 Aoû 2005, 18:32
par gamecuber » 18 Aoû 2005, 18:32
"N_comme_Nul" a écrit:Encore faudrait-il que -1 soit un entier naturel
Ah oui tu as raison, il y quelque chose qui ne colle pas sur mon lien, vu qu'ils supposent au début k un entier naturel, puis qu'ils parlent du cas k<0...
-
N_comme_Nul
- Membre Relatif
- Messages: 127
- Enregistré le: 06 Aoû 2005, 22:00
-
 par N_comme_Nul » 18 Aoû 2005, 18:38
par N_comme_Nul » 18 Aoû 2005, 18:38
Autant/au temps pour moi.
( Et pas besoin d'être sarcastique :hum: .)
PS : le lien fait mention du calcul du coeff binomial pour des entiers naturels k et n ... le cas "k<0" me laisse perplexe ... il peut arriver à un entier naturel d'être négatif ? :briques:
-
gamecuber
- Membre Naturel
- Messages: 36
- Enregistré le: 01 Mai 2005, 01:14
-
 par gamecuber » 18 Aoû 2005, 19:07
par gamecuber » 18 Aoû 2005, 19:07
"N_comme_Nul" a écrit:il peut arriver à un entier naturel d'être négatif ?
Rarement

C'est pour cela que j'ai dit juste avant que "quelque chose ne collait pas sur mon lien"

-
N_comme_Nul
- Membre Relatif
- Messages: 127
- Enregistré le: 06 Aoû 2005, 22:00
-
 par N_comme_Nul » 18 Aoû 2005, 19:18
par N_comme_Nul » 18 Aoû 2005, 19:18
Disons alors que :
Pour tous entiers naturels

et

:
[CENTER]
=\left\{\begin{array}{l}\frac{n!}{k!(n-k)}\qquad\text{si }k\leq n\\0\qquad\text{si }k>n\end{array}\right.)
[/CENTER]
et pour tout entier naturel

et pour tout entier
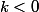
:
[CENTER]
=0)
[/CENTER]
:hein:
PS : désolé alors pour la (mauvaise) interprétation de ton post gamecuber.
-
Anonyme
 par Anonyme » 18 Aoû 2005, 19:26
par Anonyme » 18 Aoû 2005, 19:26
"N_comme_Nul" a écrit:Disons alors que :
Pour tous entiers naturels

et

:
[CENTER]
=\left\{\begin{array}{l}\frac{n!}{k!(n-k)}\qquad\text{si }k\leq n\\0\qquad\text{si }k>n\end{array}\right.)
[/CENTER]
et pour tout entier naturel

et pour tout entier
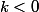
:
[CENTER]
=0)
[/CENTER]
C'est plus clair ainsi !
"N_comme_Nul" a écrit:PS : désolé alors pour la (mauvaise) interprétation de ton post gamecuber.
Pas de problème !

a+
-
gamecuber
- Membre Naturel
- Messages: 36
- Enregistré le: 01 Mai 2005, 01:14
-
 par gamecuber » 18 Aoû 2005, 19:27
par gamecuber » 18 Aoû 2005, 19:27
oups j'ai oublié de m'identifier... le non-inscrit, c'était moi! :)
PS : oublie pas le point d'exclamation devant (n-k) ;)
-
Anonyme
 par Anonyme » 18 Aoû 2005, 19:32
par Anonyme » 18 Aoû 2005, 19:32
N comme Nul, tu oublies le cas n<0, non?
-
N_comme_Nul
- Membre Relatif
- Messages: 127
- Enregistré le: 06 Aoû 2005, 22:00
-
 par N_comme_Nul » 18 Aoû 2005, 20:58
par N_comme_Nul » 18 Aoû 2005, 20:58
Salut !
"N comme Nul, tu oublies le cas n<0, non?"
[INDENT]Ben pour le cas
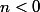
, on va prendre la définition donnée dans le lien donné par gamecuber (elle est étendue au cas où n est un complexe ):[/INDENT]
[CENTER]
(n-2)\cdots (n-k+1)}{k!})
[/CENTER]
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
