Salut,
Si effectivement l'énoncé est formulé en terme de "
Donner une minoration de 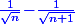
" alors c'est effectivement "plutôt mal dit" vu que si on regarde la définition de ce qu'est "un minorant d'une suite
_{n\geq\!0})
", ben il faut évidement que ce soit un truc qui dépend pas de

. Et comme tu l'a très bien vu toi même, ici, un minorant qui ne dépendrait pas de

, ben c'est assez clairement 0 et c'est tout.
Mais bon, il faut aussi savoir lire correctement (et un peu "entre les lignes") et/ou comprendre ce qui est attendu : là, déjà, on te demande pas un minorant de
la suite _{n\geq 0})
, mais un minorant
du nombre 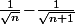
ce qui signifie (ou laisse sous entendre) que le minorant à le droit de dépendre de

.
Mais là où c'est vicieux, c'est que si le minorant à le droit de dépendre de

, ben tu pourrait tout aussi bien ne pas te faire chier et répondre qu'un minorant de
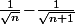
c'est . . . lui même . .
Sauf que bien sûr c'est pas ça qui est attendu comme réponse : on te demande un minorant dépendant de

certes, mais aussi "le plus simple possible".
