Une injection ?

[infernaleur]

Salut,
J'aurais besoin d'une indication pour cette exercice.

(Dans la suite les intervalles que j’ai écris ne contiennent que des entiers naturels)

Pour tout ensemble A tel que et
Montrer que

D'après mon prof il faudrait utiliser le théorème suivant :
"soit .
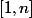
Il existe une injection de dans si et seulement si "

J'ai donc posé avec .
donc il existe une injection de A dans [1,2n]

On définit :
qui est injective.
pour y un entier naturel non nul fixé on pose

Mais après je ne vois pas que faire après et comment utiliser l'injectivité de f ...

Merci de votre aide !

[Ben314]

Salut,
Je regarderais ensuite ce que tu propose, mais le résultat me semble quand même on ne peut plus crétin vu que si on prend n+1 entiers entre 1 et 2n, ben on est obligé d'en prendre deux qui se suivent (sinon la somme des écart serait supérieure à 2n) et évidement, deux entiers qui se suivent, leur pgcd est égal à 1.

Edit : modulo bien sûr que ton "x^y" désigne le pgcd de x et de y...

[infernaleur]

désoler de répondre aussi tard, oui "x^y" désigne bien le PGCD.

[infernaleur]

Je suis daccord avec toi c'est ce que je me disais avant d’entamer l'exo, mais je vois pas comment utiliser le théorème pour résoudre cette exercice.
Surement poser une application injective particulière qui fait intervenir le PGCD puis l'évaluer en une valeur particulière qui donnerait le résultat ?