Une colle?!

[Anonyme]

Bonjour a tous, je colle sur ce petit probleme

x^y = y^x avec le couple (x,y) appartenant a N étoile.

J'ai pas mal cherché, composer avec ln, utiliser l'arithmétique ...mais rien...
please HELP merci :) niveau : mpsi

[Mikou]

http://www.maths-forum.com/showthread.php?t=13435&page=1
cf demo de quidam.
nb : il existe d'autre methode pour solutioner le pb.

[Anonyme]

Ah mErci j'avais pa vu auparavant, je vais étudier celle la merci

[Anonyme]

Si quelqu'un aurait une autre démonstration, ou tuyaux ^^ Merci

[Nota-Bene19]

Salut;

c pas facile de trouver les solutions , mais je te donne : (x,y)=(2,4) ou (4,2) ou (1,1)....et je ne crois pas qu'il y en a d'autres .(si x=y .c évident).

Au revoir!!!

[Anonyme]

Javais trouvé cela au premier abord, mais il yen a d'autres ... voir la méthode de QUidam ...Si quelqu'un a quelquechose

[yos]

On peut le faire par l'arithmétique : on suppose que les entiers x, y vérifient :
, donc a=1.
Ainsi .
-Si d=1, alors b=1 impossible.
-Si d>2, alors (la dernière inégalité est immédiate par récurrence sur b). Impossible à nouveau.
-Reste le cas d=2. On a donc mais dés que (récurrence à nouveau). D'où b=2.

En résumé, a=1 et b=d=2, donc x=2 et y=4.

En aiguisant un peu la méthode, on obtient que les solutions dans de l'équation 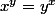(avec 0<x<y) sont les couples où n est un entier naturel. En faisant n=1 on retrouve (2,4).
C'est un bel exercice je trouve.

[Nota-Bene19]

Salut;

je ne suis pas d'acord avec toi Yos :

- on cherche seulement les entiers .

- comment choisir n pour que (4,2) soit une solution [ elle l'est car 4²=2^4 ].

Au revoir.

Pour toi N8love :

quelles sont les autres solutions qui a trouvé Quidam ?.donne moi les !!!.

A+.

[yos]

Salut;

- on cherche seulement les entiers .

C'est ce que j'ai fait mais j'ai rajouté une remarque sur un problème plus général (mes 4 dernières lignes).

- comment choisir n pour que (4,2) soit une solution

n=1 comme je l'ai écrit mais ne te préoccupe pas de mes 4 dernières lignes. La démonstration du fait qu'il n'y a pas d'autres solutions que(2,4) (ou (4,2), c'est ce qui précède.