Aide colle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
maestro_
- Membre Naturel
- Messages: 14
- Enregistré le: 30 Déc 2014, 18:21
-
 par maestro_ » 16 Jan 2015, 14:07
par maestro_ » 16 Jan 2015, 14:07
bonjour Soit la fonction f définie sur IR+ par f (x)=

Montrer que f est uniformément continue sur IR+. quelqu'un connaitrait la méthode svp pour m'aider merci
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 16 Jan 2015, 14:12
par Monsieur23 » 16 Jan 2015, 14:12
Aloha,
Tu peux commencer par montrer que pour tous x,y dans R+,

« Je ne suis pas un numéro, je suis un homme libre ! »
-
charles xang
- Membre Naturel
- Messages: 67
- Enregistré le: 09 Nov 2014, 10:45
-
 par charles xang » 16 Jan 2015, 14:29
par charles xang » 16 Jan 2015, 14:29
Monsieur23 a écrit:Aloha,
Tu peux commencer par montrer que pour tous x,y dans R+,


=

suis je sur la bonne voie?
-
charles xang
- Membre Naturel
- Messages: 67
- Enregistré le: 09 Nov 2014, 10:45
-
 par charles xang » 16 Jan 2015, 14:54
par charles xang » 16 Jan 2015, 14:54
charles xang a écrit:
=

suis je sur la bonne voie?
besoin d'aide svp ^^
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 16 Jan 2015, 14:58
par Luc » 16 Jan 2015, 14:58
maestro_ a écrit:bonjour Soit la fonction f définie sur IR+ par f (x)=

Montrer que f est uniformément continue sur IR+. quelqu'un connaitrait la méthode svp pour m'aider merci
Pour compléter la réponse de Monsieur23, voici une autre approche:
- que vaut la dérivée de f? quand est-elle grande? petite?
- Trouver un intervalle intéressant sur lequel f est lipschitzienne (donc uniformément continue)
- Conclure (attention il y a un piège)
Luc
-
charles xang
- Membre Naturel
- Messages: 67
- Enregistré le: 09 Nov 2014, 10:45
-
 par charles xang » 16 Jan 2015, 15:32
par charles xang » 16 Jan 2015, 15:32
Luc a écrit:Pour compléter la réponse de Monsieur23, voici une autre approche:
- que vaut la dérivée de f? quand est-elle grande? petite?
- Trouver un intervalle intéressant sur lequel f est lipschitzienne (donc uniformément continue)
- Conclure (attention il y a un piège)
Luc
dérivée c'est

quand x->0 la dérivée est grande x-->+00 dérivée est petite
je doit chercher donc k>0 avec [a,+oo[ on obtient |

|=0 :

-
charles xang
- Membre Naturel
- Messages: 67
- Enregistré le: 09 Nov 2014, 10:45
-
 par charles xang » 16 Jan 2015, 15:38
par charles xang » 16 Jan 2015, 15:38
charles xang a écrit:dérivée c'est

quand x->0 la dérivée est grande x-->+00 dérivée est petite
je doit chercher donc k>0 avec [a,+oo[ on obtient |

|=0 :

c'est tout?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 16 Jan 2015, 16:15
par Luc » 16 Jan 2015, 16:15
charles xang a écrit:dérivée c'est

quand x->0 la dérivée est grande x-->+00 dérivée est petite
Oui
charles xang a écrit:je doit chercher donc k>0 avec [a,+oo[ on obtient |

|=0 :

Vrai mais inutile ici.
Je te rappelle le but de l'exercice : montrer l'uniforme continuité de f, c'est-à-dire trouver
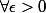
un
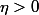
tel que
-f(y)|<\epsilon)
-
charles xang
- Membre Naturel
- Messages: 67
- Enregistré le: 09 Nov 2014, 10:45
-
 par charles xang » 16 Jan 2015, 16:34
par charles xang » 16 Jan 2015, 16:34
Luc a écrit:Oui
Tel quel ça ne veut rien dire. Les quantificateurs?
Quelle majoration et quel théorème utilises tu pour montrer que f est lipschitzienne sur cet intervalle (à préciser).
charles xang a écrit:j'en déduis |

|=|x-y|/
=0)
un
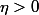
tel que
-f(y)|<\epsilon)
pour l'intervalle je prend ]0;1] ?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 16 Jan 2015, 16:50
par Luc » 16 Jan 2015, 16:50
charles xang a écrit:
pour l'intervalle je prend ]0;1] ?
est-ce que
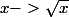
est lipschitizenne sur cet intervalle?
-
charles xang
- Membre Naturel
- Messages: 67
- Enregistré le: 09 Nov 2014, 10:45
-
 par charles xang » 16 Jan 2015, 17:00
par charles xang » 16 Jan 2015, 17:00
Luc a écrit:est-ce que
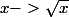
est lipschitizenne sur cet intervalle?
oui elle l'est je pense on peut pas faire
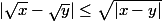
donc on a:
x+y-2
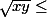
|x-y|
et je fais le cas
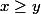
et on a

donc il existe
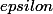

je galère sur l'autre cas merci
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 16 Jan 2015, 17:56
par Luc » 16 Jan 2015, 17:56
charles xang a écrit:oui elle l'est je pense
et non...
par contre, elle est uniformément continue (c'est le but de l'exercice de le monter).
Le reste concerne la méthode n°1, je laisse donc Monsieur23 y répondre.
Tu as fait un dessin?
Luc
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 16 Jan 2015, 17:57
par mehdiphone » 16 Jan 2015, 17:57
Luc a écrit:et non...
par contre, elle est uniformément continue (c'est le but de l'exercice de le monter).
Tu as fait un dessin?
Luc
euh non ? mais ce que j'ai fait est ce correcte ? merci
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 16 Jan 2015, 17:58
par mehdiphone » 16 Jan 2015, 17:58
[quote="mehdiphone"]euh non j'ai vraiment du mal sur ce chapitre que j'ai en colle mardi prochain ..... pourquoi un dessin?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 16 Jan 2015, 18:02
par Luc » 16 Jan 2015, 18:02
mehdiphone a écrit:euh non ? mais ce que j'ai fait est ce correcte ? merci
Ce que tu as écrit est très mal écrit, donc je ne comprends rien... Précise les variables et les quantificateurs, ce que tu sais et ce que tu veux montrer.
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 16 Jan 2015, 18:17
par mehdiphone » 16 Jan 2015, 18:17
charles xang a écrit:oui elle l'est je pense on peut pas faire
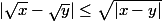
donc on a:
x+y-2
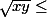
|x-y|
et je fais le cas
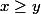
et on a

donc il existe
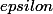

je galère sur l'autre cas merci
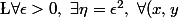\in {\mathbb R^+}^2,\ |x-y|\leq \epsilon^2 \Longrightarrow |\sqrt x -\sqrt y|\leq \sqrt {|x-y|}\leq \sqrt {\epsilon ^2}=\epsilon)
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 16 Jan 2015, 18:33
par Luc » 16 Jan 2015, 18:33
mehdiphone a écrit: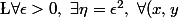\in {\mathbb R^+}^2,\ |x-y|\leq \epsilon^2 \Longrightarrow |\sqrt x -\sqrt y|\leq \sqrt {|x-y|}\leq \sqrt {\epsilon ^2}=\epsilon)
oui! ça a l'air correct. comment justifies-tu l' inégalité
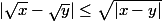
?
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 16 Jan 2015, 18:36
par mehdiphone » 16 Jan 2015, 18:36
Luc a écrit:oui! ça a l'air correct. comment justifies-tu l' inégalité
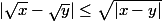
?
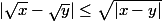
donc on a:
x+y-2
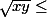
|x-y|
et je fais le cas
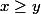
et on a

donc il existe
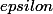

maisi l'autre cas je n'y arrive pas
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 16 Jan 2015, 18:40
par paquito » 16 Jan 2015, 18:40
Dans le cadre de la topologie des espaces métriques. Sur
=|x-y|)
, on dispose du théorème suivant:toute fonction continue sur un compact [a; b] est uniformément continue sur [a; b]. pour démontrer ce résultat fondamental, il faut déjà écrire correctement la définition de l'uniforme continuité, puisque la démonstration se fait par l'absurde et qu'il faut donc écrire la négation correctement. Ce théorème est fondamental pour prouver que
dt=F(b)-F(a))
-
mehdiphone
- Membre Naturel
- Messages: 46
- Enregistré le: 31 Oct 2014, 16:30
-
 par mehdiphone » 16 Jan 2015, 18:41
par mehdiphone » 16 Jan 2015, 18:41
paquito a écrit:Dans le cadre de la topologie des espaces métriques. Sur
=|x-y|)
, on dispose du théorème suivant:toute fonction continue sur un compact [a; b] est uniformément continue sur [a; b]. pour démontrer ce résultat fondamental, il faut déjà écrire correctement la définition de l'uniforme continuité, puisque la démonstration se fait par l'absurde et qu'il faut donc écrire la négation correctement. Ce théorème est fondamental pour prouver que
dt=F(b)-F(a))
c'est pas bon?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
 Montrer que f est uniformément continue sur IR+. quelqu'un connaitrait la méthode svp pour m'aider merci
Montrer que f est uniformément continue sur IR+. quelqu'un connaitrait la méthode svp pour m'aider merciMontrer que f est uniformément continue sur IR+. quelqu'un connaitrait la méthode svp pour m'aider merci
quand x->0 la dérivée est grande x-->+00 dérivée est petite
|=0 :
=|x-y|) , on dispose du théorème suivant:toute fonction continue sur un compact [a; b] est uniformément continue sur [a; b]. pour démontrer ce résultat fondamental, il faut déjà écrire correctement la définition de l'uniforme continuité, puisque la démonstration se fait par l'absurde et qu'il faut donc écrire la négation correctement. Ce théorème est fondamental pour prouver que
, on dispose du théorème suivant:toute fonction continue sur un compact [a; b] est uniformément continue sur [a; b]. pour démontrer ce résultat fondamental, il faut déjà écrire correctement la définition de l'uniforme continuité, puisque la démonstration se fait par l'absurde et qu'il faut donc écrire la négation correctement. Ce théorème est fondamental pour prouver quedt=F(b)-F(a))
, on dispose du théorème suivant:toute fonction continue sur un compact [a; b] est uniformément continue sur [a; b]. pour démontrer ce résultat fondamental, il faut déjà écrire correctement la définition de l'uniforme continuité, puisque la démonstration se fait par l'absurde et qu'il faut donc écrire la négation correctement. Ce théorème est fondamental pour prouver que
