En ce qui concerne "un peu plus grand" : on commence par évacuer
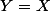
(on vérifie aisément que
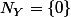
et
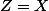
)
On considère maintenant
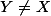
Le principal point ici est d'être sûr qu'on puisse définir une forme linéaire
continue dont le noyau est

. D'où une condition nécessaire :

est l'image réciproque de

, image réciproque d'un fermé, donc doit être fermé.
Après on suppose que
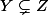
: cela justifie l'existence de
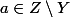
La définition de l'espace
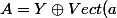)
est alors possible.
On peut alors expliciter une forme linéaire particulière : si
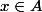
, alors
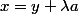
de façon unique grâce à la somme directe. Du coup, on peut définir

avec
=\lambda)
et le noyau est clairement

Il faut alors vérifier alors que la forme linéaire est bornée : avec
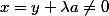
, on calcule
|}{||x||}=\dfrac{|\lambda|}{||y+\lambda a||}=\dfrac{1}{||\frac{y}{\lambda}+ a||})
C'est là que la fermeture de Y joue : en appelant
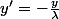
, le démoninateur s'écrit
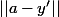
et cette valeur est supérieure à la distance de

à

Comme

est fermé, cette distance n'est pas nulle, ce qui permet de borner g : qui par conséquent est continue.
Forme linéaire bornée, donc continue, donc dans le dual.
Ce n'est qu'à partir d'ici qu'on peut utiliser Hahn-Banach : le théorème dit que toute forme linéaire continue sur un sous-espace vectoriel peut être prolongé de façon continue, en conservant la même norme d'application linéaire sur l'espace tout entier, ce qui permet de prolonger

dans

Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
