Trouver les racines d'un polynôme
19 messages
- Page 1 sur 1
Trouver les racines d'un polynôme
Bonsoir à tous,
J'aimerais savoir comment montrer qu'un polynôme de la forme X^3 +pX + q admet 3 racines réelles distinctes ?
- Selon moi, on sait que tout polynôme de degré impaire admet au moins une racine réelle
-On peur également passer par l'inégalité des accroissements finis pour justifier l'existence d'une racine
Bon voilà un peu ce que je vois
Merci d'avance !
J'aimerais savoir comment montrer qu'un polynôme de la forme X^3 +pX + q admet 3 racines réelles distinctes ?
- Selon moi, on sait que tout polynôme de degré impaire admet au moins une racine réelle
-On peur également passer par l'inégalité des accroissements finis pour justifier l'existence d'une racine
Bon voilà un peu ce que je vois
Merci d'avance !
Re: Trouver les racines d'un polynôme
Salut,
Ben c'est on ne peut plus couillon : tu étudie simplement les différents tableaux de variations possible de la fonction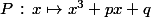 .
.
=3x^2\!+\!p) donc si
donc si 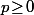 , la fonction
, la fonction  est strictement croissante sur
est strictement croissante sur  et ne s’annule qu'une fois.
et ne s’annule qu'une fois.
Si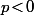 , la fonction
, la fonction  est croissante sur
est croissante sur 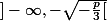 puis décroissante sur
puis décroissante sur 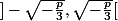 puis croissante sur
puis croissante sur 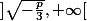 donc P s'annulle trois fois ssi
donc P s'annulle trois fois ssi \!>\!0) et
et \!<\!0) c'est à dire en fait (mini calcul à faire) ssi
c'est à dire en fait (mini calcul à faire) ssi 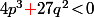 (*)
(*)
(*) Et pas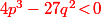 comme je l'avais écrit dans la première version.
comme je l'avais écrit dans la première version.
Ben c'est on ne peut plus couillon : tu étudie simplement les différents tableaux de variations possible de la fonction
Si
(*) Et pas
Modifié en dernier par Ben314 le 14 Sep 2018, 21:53, modifié 5 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Trouver les racines d'un polynôme
(1) q est aussi grand positif au négatif qu'on veut, il crée un décalage qui rend le résultat peu certain
(2) s'il admet 3 racine réelles, sa dérivée en admet 2 ?
(2) s'il admet 3 racine réelles, sa dérivée en admet 2 ?
Re: Trouver les racines d'un polynôme
j'ai pas fait le calcul mais à mon avis c'est 4p^3+27 q^2 sinon avec p<0 l'expression aurait toujours le meêm signe.
Re: Trouver les racines d'un polynôme
Oui, je me suis gouré en faisant le calcul : je rectifie...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Trouver les racines d'un polynôme
Mais, est ce qu'il y'a des formules pour calculer la somme des racines ou la somme du produit des racines ?
Ou bien si quelqu'un a un pdf qui en parle, me transmettre me ferait du bien, je cherché sur Google mais les résultats concernent les polynômes de degré 2
Merci d'avance !
Ou bien si quelqu'un a un pdf qui en parle, me transmettre me ferait du bien, je cherché sur Google mais les résultats concernent les polynômes de degré 2
Merci d'avance !
Re: Trouver les racines d'un polynôme
Bonjour Y a rien de compliqué
Tu écris p(x)=(x-a)*(x-b)*(x-c) tu développes et tu va voir apparaitre la somme, le produit et puis ab+bc+ca.
Par contre "la somme du produit des racines" c'est quoi ce machin là?
Tu écris p(x)=(x-a)*(x-b)*(x-c) tu développes et tu va voir apparaitre la somme, le produit et puis ab+bc+ca.
Par contre "la somme du produit des racines" c'est quoi ce machin là?
Re: Trouver les racines d'un polynôme
Par exemple si on a x^3 - 3x -1= 0
Montrer que l équation admet trois racines distinctes a, b, c
Montrer que a + b + c = 0 et a^2bc + ab^2c + abc^2 = 0
A travers le tableau de variation j'ai pu montrer l'existence des trois racines
Mais je veux des pistes pour résoudre les sommes.
Merci !
Montrer que l équation admet trois racines distinctes a, b, c
Montrer que a + b + c = 0 et a^2bc + ab^2c + abc^2 = 0
A travers le tableau de variation j'ai pu montrer l'existence des trois racines
Mais je veux des pistes pour résoudre les sommes.
Merci !
Re: Trouver les racines d'un polynôme
développe (x-a)(x-b)(x-c) et tu verras apparaître ces expressions symétriques en les racines a,b,c : c'est ce qu'on appelle les relations coefficients racines!
https://fr.wikipedia.org/wiki/Relations ... et_racines
https://fr.wikipedia.org/wiki/Relations ... et_racines
Re: Trouver les racines d'un polynôme
Georges10 a écrit:Mais je veux des pistes pour résoudre les sommes.
La piste je te l'ai donnée et LB2 le rappelle. Fais ce qu'on te dit, sinon tu veux la solution?
Re: Trouver les racines d'un polynôme
Façon 1 de résoudre ça sans des équation de degré 3, et en utilisant des notions proches du TAF.
on a de la chance, le polynôme est réel à coefficients réels, on peut le confondre avec la fonction polynôme associée.
X^3 +pX + q admet 3 racines réelles distinctes ?
on connait la forme d'un polynôme de degré 3 et pour sa représentation graphique coupe 3 fois l'axe des abscisses, il faut qu'ai ait 2 extremums locaux, donc que sa dérivée s'annule 2 fois en des abscisses différentes.
soit f(x) = x^3 +px + q
f'(x)=3x²+p
on remarque que le fait que f' s'annule dépend beaucoup de la valeur de p et donc,
-> résol niveau bac
où est le TAF ?
TAF-Roll-TVI se démontrent en cascade à partir du TVI issu de la continuité.
et une fois qu'on a les 2 valeurs pour les quelles la dérivée s'annule, il faut encore que la fonction prenne des signes différents pour avoir les 3 racines demandées (TVI).
on a de la chance, le polynôme est réel à coefficients réels, on peut le confondre avec la fonction polynôme associée.
X^3 +pX + q admet 3 racines réelles distinctes ?
on connait la forme d'un polynôme de degré 3 et pour sa représentation graphique coupe 3 fois l'axe des abscisses, il faut qu'ai ait 2 extremums locaux, donc que sa dérivée s'annule 2 fois en des abscisses différentes.
soit f(x) = x^3 +px + q
f'(x)=3x²+p
on remarque que le fait que f' s'annule dépend beaucoup de la valeur de p et donc,
-> résol niveau bac
où est le TAF ?
TAF-Roll-TVI se démontrent en cascade à partir du TVI issu de la continuité.
et une fois qu'on a les 2 valeurs pour les quelles la dérivée s'annule, il faut encore que la fonction prenne des signes différents pour avoir les 3 racines demandées (TVI).
Re: Trouver les racines d'un polynôme
Pour aviateur : Façon 2 de voir (sans image, imagilive est HS).
J'aimerais savoir comment montrer qu'un polynôme de la forme X^3 +pX + q admet 3 racines réelles distinctes ?
X^3 +pX + q : a une forme "⋂⋃" quand il a 3 racines réelles
si y1 et y2 sont les valeurs des deux extremums locaux
X^3 +pX + q +|y1]+|y2] n'a pas de racine
donc on a pas 3 racines pour toute valeur de q
donc X^3 +pX + q n'admet pas 3 racine réelles distinctes pour toute valeur de q.
J'aimerais savoir comment montrer qu'un polynôme de la forme X^3 +pX + q admet 3 racines réelles distinctes ?
X^3 +pX + q : a une forme "⋂⋃" quand il a 3 racines réelles
si y1 et y2 sont les valeurs des deux extremums locaux
X^3 +pX + q +|y1]+|y2] n'a pas de racine
donc on a pas 3 racines pour toute valeur de q
donc X^3 +pX + q n'admet pas 3 racine réelles distinctes pour toute valeur de q.
Re: Trouver les racines d'un polynôme
Bonjour,
l'idée de pascal16 est rédigée par exemple dans l'exercice 148 du livre Calculus (Tosel) dont voici un énoncé succinct :
On s'intéresse au nombre de racines réelles de l'équation f(x)=0 avec f(x)=x^3+px+q, p et q étant deux réels.
Remarquons déjà que f est continue, de limite - l'infini en - l'infini et + l'infini en plus l'infini, donc admet au moins une racine réelle par TVI
a) Si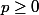 , f est strictement croissante sur R, donc admet au plus une racine, donc exactement une racine.
, f est strictement croissante sur R, donc admet au plus une racine, donc exactement une racine.
b) Si p<0, f admet le tableau de variations suivant : Croissant / Décroissant / Croissant, avec les extrema locaux égaux à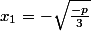 et
et 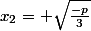
On calculef(x_2)=q^2+\frac{4p^3}{27}) dont le signe indique si f(x_1) et f(x_2) sont de même signe ou de signe opposé
dont le signe indique si f(x_1) et f(x_2) sont de même signe ou de signe opposé
c) Si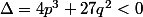 , ce qui impose p<0, alors il y a trois racines réelles distinctes
, ce qui impose p<0, alors il y a trois racines réelles distinctes
Si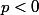 et
et 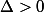 , il y a une seule racine réelle
, il y a une seule racine réelle
Si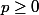 et
et 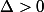 , il y a une seule racine réelle
, il y a une seule racine réelle
Si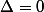 , soit
, soit 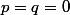 et il y a une seule racine réelle (
et il y a une seule racine réelle ( ), soit
), soit 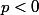 et il y a exactement deux racines réelles
et il y a exactement deux racines réelles
EDIT : Ben l'a déjà dit en fait... en un peu plus court
l'idée de pascal16 est rédigée par exemple dans l'exercice 148 du livre Calculus (Tosel) dont voici un énoncé succinct :
On s'intéresse au nombre de racines réelles de l'équation f(x)=0 avec f(x)=x^3+px+q, p et q étant deux réels.
Remarquons déjà que f est continue, de limite - l'infini en - l'infini et + l'infini en plus l'infini, donc admet au moins une racine réelle par TVI
a) Si
b) Si p<0, f admet le tableau de variations suivant : Croissant / Décroissant / Croissant, avec les extrema locaux égaux à
On calcule
c) Si
Si
Si
Si
EDIT : Ben l'a déjà dit en fait... en un peu plus court
Re: Trouver les racines d'un polynôme
Le but est bien de comprendre la démarche qui aboutie au résultat pour être capable de réutiliser la démarche (et pas le résultat) dans une situation inconnue.
Ainsi, un exercice type Capes est retrouvé dans un anneau (commutatif) une série de conditions nécessaires pour utiliser le calcul du delta dans la résolution d'une équation du second degré. On peut retrouver la notion de "racine de delta" comme dans C : la première venue fait l'affaire.
Ainsi, un exercice type Capes est retrouvé dans un anneau (commutatif) une série de conditions nécessaires pour utiliser le calcul du delta dans la résolution d'une équation du second degré. On peut retrouver la notion de "racine de delta" comme dans C : la première venue fait l'affaire.
Re: Trouver les racines d'un polynôme
pascal16 a écrit:Ainsi, un exercice type Capes est retrouvé dans un anneau (commutatif) une série de conditions nécessaires pour utiliser le calcul du delta dans la résolution d'une équation du second degré. On peut retrouver la notion de "racine de delta" comme dans C : la première venue fait l'affaire.
Qu'est que ça veut dire? Tu peux faire une explication de texte?
Re: Trouver les racines d'un polynôme
Tu peux ouvrir une nouvelle discussion, on est loin du post initial.
[PS] : le premier post parlait du TAF, applicable sur la fonction polynôme, on avait un polynôme réel à coefficients réels, on pouvait confondre les deux.
Les solutions avec la factorisation ont l'avantage d'aller beaucoup plus loin dans la résolution via un polynôme formel qui est un cap à passer en prépa.
[PS] : le premier post parlait du TAF, applicable sur la fonction polynôme, on avait un polynôme réel à coefficients réels, on pouvait confondre les deux.
Les solutions avec la factorisation ont l'avantage d'aller beaucoup plus loin dans la résolution via un polynôme formel qui est un cap à passer en prépa.
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
