On cherche à construire une boite rectangulaire (parallélépipède rectangle) la plus légère
possible (avec le minimum de matière) dont le volume intérieur sera
48 ,la surlace supposée d'épaisseur nulle s. quelles doivent etre ses dimensions : largeur (x), longueur (z), et hauteur (y)? La boite est ouverte en haut, mais
Il y a tout de meme un pourtour de largeur 1 qui solidifie la structure.
Notre boîte s'apparente en quelque sorte à une urne
Merci d'avance de vos réponses
Trouver les dimensions d'une boîte
11 messages
- Page 1 sur 1
Re: Trouver les dimensions d'une boîte
Bonjour,
tu n'as sûrement pas cherché beaucoup, même sur notre site!
vois ici https://www.maths-forum.com/superieur/taille-ideal-pour-une-boite-rectangulaire-t276706.html
tu n'as sûrement pas cherché beaucoup, même sur notre site!
vois ici https://www.maths-forum.com/superieur/taille-ideal-pour-une-boite-rectangulaire-t276706.html
Re: Trouver les dimensions d'une boîte
tournesol a écrit:Ce n'est pas la même question Pisigma.
ça je sais mais ça donne des indications pour résoudre l'exercice
Re: Trouver les dimensions d'une boîte
Pisigma a écrit:Bonjour,
tu n'as sûrement pas cherché beaucoup, même sur notre site!
vois ici https://www.maths-forum.com/superieur/taille-ideal-pour-une-boite-rectangulaire-t276706.html
ça y est, j'ai finalisé la démo, tu peux y jeter un coup d'oeil Matt2000d
Re: Trouver les dimensions d'une boîte
Théorème Soient 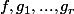 des fonctions réelles de classe C1 sur un ouvert U de
des fonctions réelles de classe C1 sur un ouvert U de  .
.
On note X l'ensemble des x U tels que:
U tels que:
=...=g_n(x)=0)
Si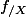 admet un extremum local en a et si les formes linéaires
admet un extremum local en a et si les formes linéaires ,.., dg_r(a)) sont indépendantes
sont indépendantes
alors il existe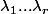 dans
dans  tels que:
tels que:
=\lambda_1 dg_1(a)+...+ \lambda_r dg_r(a))
autrement dit , les formes linéaires,dg_1(a),..dg_r(a)) sont liées.
sont liées.
on pose alors: f(x,y,z)=2xy+2yz+xz+2x+2z et g(x)=xyz-48
On calcule leurs différentielles:
 = \left( \begin{array} {c} <br />2y+z+2 \cr<br />2x+2z \cr<br />x+2y+2 \cr<br />\end{array} \right))
 = \left( \begin{array} {c} <br />yz \cr<br />xz \cr<br />xy \cr<br />\end{array} \right))
On écrit deux déterminants mineurs nuls pour exprimer que df et dg sont colinéaires
On note X l'ensemble des x
Si
alors il existe
autrement dit , les formes linéaires
on pose alors: f(x,y,z)=2xy+2yz+xz+2x+2z et g(x)=xyz-48
On calcule leurs différentielles:
On écrit deux déterminants mineurs nuls pour exprimer que df et dg sont colinéaires
Re: Trouver les dimensions d'une boîte
Bonjour mathelot,
Je vois que tu as adopté la méthode que j'ai utilisée dans l'autre exercice.
Je vois que tu as adopté la méthode que j'ai utilisée dans l'autre exercice.
Re: Trouver les dimensions d'une boîte
Tiens GBZM as tu une méthode (moins laborieuse que la mienne ) pour démontrer que le point critique est bien un minimum global de f sur l'ouvert
R+*xR+* ?
R+*xR+* ?
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
