Bonsoir
Soient R et R' deux rectangles du plan complexe de longueurs de côtés respectives a

b et a'

b' .
1) Montrer que si

, alors il existe une bijection conforme du plan qui envoie R sur R' en respectant les côtés.
On considère maintenant R = [0,a] x [0,1] et R' = [0,a'] x [0,1] et une bijection conforme

: R

R'
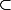
U' (où U et U' sont des ouverts) qui envoie R sur R' en respectant les côtés.
2) Montrer que Aire(R') = a' =
|^2 dxdy) 3)
3) Pour tout y

[0,1], on considère la courbe
=f(t+iy))
où t

[0,a]. En intégrant la longueur de
)
sur [0,1] montrer que a'
| dxdy)
L'exercice comporte d'autres questions, mais je prendrai le temps de les poser un peu plus tard...
Pour la 1) je peux dire que

, mais je ne sais pas comment bien rédiger pour répondre à la question. Pour le reste ... j'aimerais bien un peu d'aide...même si ça n'a pas l'air terriblement compliqué. Je n'arrive pas à voir à quoi correspondent (géométriquement) les termes sous les doubles intégrales... si vous pouviez m'éclairer quelque peu! merci par avance
