Nouvelle démo pour l'aire d'un rectangle

[duchere]

Bonjour, j'avais fait un post il y a peu sur l'aire d'un rectangle avec une démo un peu compliquée....

Bon, alors voici ce que j'ai de mieux....

Soit l'aire d'un rectangle de cotés et

L'axiome de départ est le suivant : et

Soit


Or,
Donc

Donc

Donc

La dérivée de A est donc constante, et on sait qu'elle n'est pas nulle.

Donc

De la même manière, on trouve

On a donc finalement

De plus,

Donc

Cette démo permet de ne pas s'embeter avec des p/q et Q qui est dense dans R , etc....

Jean

[Nicolas_75]

Bonjour,

Dans la démonstration, il faut remplacer par . Du moins si j'ai bien compris. Et encore, en 0, c'est uniquement une dérivée à droite.

Au-delà de ce point "de détail", il y a quelques problèmes de fond.

Je comprends que ton problème est le suivant.
Soit une fonction définie sur vérifiant :
(i)
(ii)
Alors montrer que :


Problème 1 : sans le dire, tu supposes que est dérivable à droite en 0, partiellement par rapport aux deux coordonnées.

Problème 2 : en conséquence, tu ne peux prouver que la dérivabilité à droite de

Problème 3 : tu écris : "La dérivée de A est donc constante, et on sait qu'elle n'est pas nulle." Qu'est-ce qui te permet de dire cela ? La fonction nulle répond à tes conditions, et est de dérivée nulle.

Sauf erreur.

Nicolas

[buzard]

Je ne vois pas ce que tu cherche à faire, l'aire d'un rectangle c'est le produit de la longueur par la largeur, et alors que peut tu bien rajouter à ca?
Le moyen le plus simple c'est encore d'utiliser la therorie de la mesure de Lebesgue :


quoi que tu fasse, equation fonctionnelle ou integrale, t'es obligé de consentir à l'arbritaire de l'aire d'un rectangle de largeur (ou hauteur) d'une unité.

En générale :



et les élements d'aire et de volume etant :



attention le theta polaire correspond au phi shperique (à cause des physiciens)


PS : j'aurai bien vue un deuxieme but

[nuage]

Salut,
on peut découper un rectangle quelconque en un nombre fini de morceaux et les réunir pour faire un carrré.
Ce qui rend inutile toute référence à l'analyse pour définir l'aire d'un polygone.
C'était dans un sujet d'agreg des années 80 (si mes souvenirs sont exacts).
Dans les axiomes manquants :
"si deux figures sont semblables alors leurs aires sont proportionnelles au carré du rapport de similitude"

A+

[duchere]

"attention le theta polaire correspond au phi shperique (à cause des physiciens)">> Cela devient comique

"Je ne vois pas ce que tu cherche à faire, l'aire d'un rectangle c'est le produit de la longueur par la largeur, et alors que peut tu bien rajouter à ca?">> POurquoi l'aire d'un rectangle est-elle une longueur fois une largeur ?

Et tout au moins avec les sommes de Rieman, l'intégrale n'est qu'une somme d'aire de rectangles...
Utiliser l'intégrale, ne serait-ce pas se mordre la queue ?
Mais sur cette question, pas tout le monde est d'accord....Donc je ne m'oppose pas, je donne un avis d'élève de terminale...

Quant à l'étalage caricaturel de tes connaissances, qui comme je l'ai dit en début de message m'a fait rire, je ne comprends le rapport avec la question...

Cependant, j'suis un élève de terminale et je ne connais rien à ce qu'ont fait les génies....
Donc, je suis prêt à entendre pleins de reproches, et l'histoire de la dérivée à droite, c'est vrai que y'a un pbm....
Donc bon... De toute facon, j'ai une autre démo... Mais celle-ci me paraissait bien plus simple....

Mais finalement pour le problème de la dérivée, si j'ai bien compris, le problème est que x ne peut pas prendre des valuers inférieures à 0 et que donc la dérivée n'est qu'à droite .. C'est ca ?
Dans ce cas, c'est vrai, j'ai tort, il ne faut pas faire apparaitre A'(0) mais A'(a) avec a différent de 0...
En effet, A(a+h,y)=A(h,y)+A(a,y)
Donc A(h,y)=A(a+h,y)-A(a,y)
Et on fait alors apparaitre A'(a) et c'est gagné (à droitre et à gauche)
Ensuite bon beh on suppose qu'elle est dérivable en a ... Bon beh... je ne sais pas comment le justifier.... ou quel axiome poser permettant de le justifier....
Cependant, je me dis la chose suivante : tout ce qu'on veut, c'est chercher une fonction qui répond aux critères qu'on s'est fixé cad A(a+b,y)=A(a,y)+A(b,y)
On cherche une fonction, pas toutes...
DOnc pourquoi ne pas supposer qu'elle est dérivable....?
Non ?
En tout cas Nicolas, tes remarques sont très vraies, et me montrent de nouveau que je suis pitoyable de non rigueur !!!

"on peut découper un rectangle quelconque en un nombre fini de morceaux et les réunir pour faire un carrré.
Ce qui rend inutile toute référence à l'analyse pour définir l'aire d'un polygone."
>>> Quelqu'un peut m'expliquer ?

"si deux figures sont semblables alors leurs aires sont proportionnelles au carré du rapport de similitude">> Je ne vois pas en quoi ca manque dans la mesure où c'est plutot ici la définition d'une similitude qui rentre en jeu ...
En effet, pour ce qui est du rectangle, si les distances sont multiplies par k, A(kx,ky)=kxky=k^2xy=k^2A(x,y)
Pour ce qui est des figures plus complexes, on encadre leurs aires entre polygones formées de carrés, on fait tendre le nombre de carré vers l'infini, et on a la même limite qui est donc l'aire de la figure...
Et comme l'aire chaque carré est multipliée par k^2, l'aire la figure est multipliée par k^2...
Je ne suis pas calir, je suis fatigué..
Je vais me coucher....

Bonne nuit à tous !

[nuage]

Salut,

"on peut découper un rectangle quelconque en un nombre fini de morceaux et les réunir pour faire un carrré.
Ce qui rend inutile toute référence à l'analyse pour définir l'aire d'un polygone."
>>> Quelqu'un peut m'expliquer ?

Si tu admet, ce qui semble raisonable, que l'aire totale de deux parties disjointes du plan est la somme de leurs aires, et l'axiome sur les similitudes (qui est équivalent à : par tout point donné il passe une parallèle unique à une droite donnée) ça permet de calculer l'aire d'un rectangle.

[Nicolas_75]

duchere,

1. Je ne suis pas convaincu de la pertinence de ton approche pour l'aire, mais je me placerai ici sur un plan purement technique de qualité de ta démonstration.

2. A ce stade, je te conseille de ne pas parler d'aire. Ton problème initial (relis ma reformulation ci-dessus) est simplement une équation fonctionnelle. Tu montres la forme des solutions, et tu décides de les appeler "aire", mais tu pourrais aussi les appeler "carottes" ou "navets".

3. Faut-il trouver une fonction ou toutes ? Toutes, bien sûr, sinon comment veux-tu définir quoi que ce soit sur cette base ?

4. Ci-dessous une tentative de nettoyage de ta démonstration, pour la rendre plus rigoureuse, tout en en respectant l'esprit.

Propriété. Les seules fonctions vérifiant :
(i) est à valeurs positives
(ii)
(iii)
(iv) est dérivable partiellement par rapport à et en tout point de
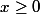
(v) est dérivable partiellement par rapport à et à droite en tout point de l'axe des abscisses ou de l'axe des ordonnées - EDIT : en tout point du demi-axe des abscisses et du demi-axe des ordonnées
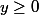
sont les fonctions où est une constante réelle positive, évidemment égale à .

Démonstration, basée sur l'idée de duchere

Tout d'abord, on déduit immédiatement de (ii) et (iii) que :
(vi) (EDIT)
(vii) (EDIT)

a. Montrons que est linéaire par rapport à
En appliquant (iii), il vient :


On fait tendre vers 0 par valeurs supérieures. En utilisant (v), on en déduit que est dérivable partiellement par rapport à à droite en tout point de et :

où désigne la dérivation à droite.
Or, d'après (iv), est dérivable partiellement par rapport à tout court en tout point de . Les dérivées partielles à gauche et à droite sont donc égales, et on a simplement :

En intégrant par rapport à , il vient :

où est une fonction définie sur
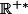
On fait tendre vers 0 par valeur supérieure. La condition (v) garantit la continuité de par rapport à à droite en tout point de l'axe des ordonnées. Donc :

Or le membre de gauche est nul d'après (vii). Donc est la fonction nulle.
Et on a montré que :

Pour simplifier les notations, notons :
On a montré que :


b. On applique maintenant le même raisonnement en dérivant par rapport à .
EDIT : En isolant dans la relation ci-dessus, et en utilisant (iv), on sait que est dérivable sur
On conclut :


Grâce à (vi) et (vii), on peut étendre à :


La condition (i) impose que soit positif. Donc :


Réciproquement, de telles fonctions vérifient les 5 conditions de la propriété.

CQFD.

Sauf erreur.

Nicolas

[nox]

wai why not...mais bon je reste quelque peu sceptique sur l'utilité de tout ca (meme si le premier post avait soulevé une discussion intéressante). Je pense juste que c'est un sujet uniquement pour s'amuser à réfléchir. L'utilité de redéfinir des choses en se passant de certains outils pour moi ca peut seulement être de comprendre comment l'idée à émergé, pour comprendre un concept à fond. C'est pour ca que le premier post était plaisant puisqu'on a pu revenir sur les bases du calcul intégral et essayer de comprendre comment on en est venu à ce type de calcul.

Maintenant l'idée n'en est pas moins intéressante et je vais suivre le développement de ce post avec intérêt. ^^
Je pense juste qu'il ne faut pas chercher à expliquer plus qu'il ne faut...pour moi on veut juste exprimer une aire de manière autre que géométrique, pour s'obliger à comprendre les formules considérées comme évidentes.
D'où la recherche de l'expression de l'aire de manière "analytique".
C'est bien ca Duchere?

PS :

Tout d'abord, on déduit immédiatement de (ii) et (iii) que :
(vi)
(vii)

il manque pas un truc la? ^^

[Nicolas_75]

nox, sur la pertinence de tout cela, je suis très réservé.
Je souhaitais juste donner (EDIT) un coup de main pour la démonstration en elle-même, de manière à ce que les réflexions de duchere soient assises sur quelque chose d'un peu plus solide.

Merci d'avoir fait remarquer (EDIT) l'oubli. Je viens de corriger.

[nox]

nox, sur la pertinence de tout cela, je suis très réservé.
Je souhaitais juste donné un coup de main pour la démonstration en elle-même, de manière à ce que les réflexions de duchere soient assises sur quelque chose d'un peu plus solide.

Pour ca entièrement d'accord la démo m'a l'air bien :happy2:

[Chimomo]

Duchere souhaitait trouver un moyen "élémentaire" de définir l'aire. Avons-nous réussi ? Je dirais non, car nous avons utilisé beaucoup de moyens topologiques et analytiques (bien qu'on ne s'en rende pas compte mais dir qu'une fonction esst dérivable à droite par rapport à une variable ça sous-entend tout un début de théorie des fonctions de plusieurs variables réelle) et du coup les myens employés n'ont plus rien d'élémentaire. je préférais la première preuve bien qu'elle nécessitait des retouches.

[duchere]

Bon, pour la démo, elle est très bien, rien à dire... mais bon... je m'applique pas car je m'en fous, mais j'admets que cela permet d'être plus clair pour communiquer avec les autres, et je vais donc essayer de m'y mettre...

Bon alors par contre, y'a pas à s'emmerder voire preque s'embrouiller avec la dérivée à droite, vu que A(h,0)=A(x0+h)-A(x0) quelque soit x0 !

Quant à chercher toutes les fonctions et non pas l'unique, je n'en vois pas l'intérêt...Peut-être suis-je trop physicien... Mais d'après moi, j'ai un but, et j'utilise le moyen le plus simple pour y parvenir.... Ainsi, une fonction dérivable me semble un moyen plus simple... Mais bon... Ca c'est qu'un avis.... :)

Quant à l'axiome de départ... Je le trouve très bon....

Personnellement, je trouve bizarre de définir les aires par les similitudes... Bien que ce soit bien plus simple en partant de là.... et que de mon axiome de départ découle très rapidement la propriété des similitudes....
Moi j'ai essayé de trouver la seule chose que je savais sur les aires....
Et la seule chose que j'ai pu dire, c'est que je voulais que l'aire soit une fonction positive, et telle que l'aire de deux domaines disjoints soit égale à la somme des aires des deux domaines...

Voilà... Mais chacun a son axiome de départ....
Et personne n'a raison !

En revanche, là où j'espère être pardonné, c'est que j'ai omis de préciser que d(y0)=0
Désolé...
Mais bon... c'était assez évident vu que A(0,y)=0 et que A(x,0)=0 et A(x,y)=xyA(1,1)+d(y)

Bon, quant à la pertinence du sujet, que ceux qui n'en trouvent pas ne viennent pas... lol... Enfin bon, ne vous obligez pas à me répondre je veux dire...
Voilà...

Jean

[duchere]

Oula....
Quelles théories ?
La dérivée et l'intégration est certes quelque chose de génial.... Mais bon... Bien que ces théories aient mis du temps, si on veut les démontrer, le cheminement n'est pas long...

C'est pas pareil que certains théorèmes d'arithmétique par exemple...

Les fonctions à doubles variables réelles, on n'en a pas besoin...

Puisque je fais les deux variables séparément

[Chimomo]

Je t'assure Duchere qu'il y a énormément de choses là-dessous et que c'est bien plus long que tu ne le crois. Tu supposes définie une bonne partie de la topologie : pour définir la continuité et la dérivabilité des fonctions de plusieurs variables réelles il faut utiliser la notion d'ouvert, de voisinage, et tout ce qui va avec. Il faut aussi la limite, qui est fondamentale. Il y a bien toute une théorie longue à mettre en oeuvre pour arriver aux théorèmes usuels qui nous parraissent bénins. Il y a bien une théorie de l'intégration, une théorie des fonctions de plusieurs variables, etc ...

Je te rappelle que le seul point de départ qu'on ait pour définir tout ça ce sont les axiomes de Zermelo-Fraenkel (bon là je m'éloigne un peu mais c'est pour montrer la vaste étendue du sujet).

Ta première démonstration utilisait (si mes souvenirs sont bons) beaucoup moins de choses.

Sinon il faut d'abord décider ce que tu supposes comme évident, et ensuite voir. Par exemple, tu utilises le fait qu'une fonction dérivable de dérivée nulle est constante, je ne sais pâs si tu sais le démontrer (c'est très facile) mais ça utilise en fait le théorème de Rolle, qui fait appel aux extrema d'une fonction qui ne sont rien d'autres que des bornes d'ensembles, et définir les bornes d'un ensemble n'est pas si facile que ça. Ce n'est qu'un exemple, mais il ya toujours plein de présupposés dans ce qu'on écrit.

[duchere]

Je suis tout à fait d'accord avec toi...

Disons juste que si on veut construire l'aire par l'analyse (?) cette méthode est bien...

Si on veut le construire avec bien moins de théories qu'ont pondu les génis avant nous, la démo d'avant était mieux....

Bien que pour x irrationnel, cela fait appel à des notions que je n'ai même pas encore abordées

[Chimomo]

Bien sur, ce que je veux dire c'est que l'aire était à la base une notion géométrique, dont on a déduit des propriétés, mais que si on veut définir mathméatiquement l'aire (que ce soit analytiquement ou autrement) ce n'est plus du tout une notion immédiate. Ceci ne retire rien à l'intérêt de tes démonstrations.

[duchere]

Oui tout à fait
Sinon, j'voulais daire qu'en y repensant, définir l'aire par les similitudes comme le disait je sais plus qui, je trouve cela pas mal finalement....