Trace nulle

par **Mohamed** » 08 Juil 2007, 19:51

[FONT=Arial Black]salut[/FONT]

voici un joli exo, je crois que c'est un oral :

soit M une matrice de

telle que

Mq elles existent deux matrices X et Y telles que :

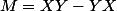good luck

par **Ledescat** » 08 Juil 2007, 21:10

J'essaierais de montrer que:

Et comme le premier est inclus dans l'autre, ça nous donnerait l'égalité des deux ev. Pour la dimension du second ça peut aller, c'est le premier qui me pose un peu problème pour le moment.

En effet, l'application :
tr: Mn(R) -> R
M-> tr(M) a pour rang 1, donc dim Ker(tr)=1, et Ker(tr) est le second ensemble.

par **tize** » 08 Juil 2007, 21:13

Ledescat a écrit:J'essaierais de montrer que:

Et comme le premier est inclus dans l'autre, ça nous donnerait l'égalité des deux ev. Pour la dimension du second ça peut aller, c'est le premier qui me pose un peu problème pour le moment.

Bonsoir,
comment montres-tu que l'ensemble de gauche est un e.v. ?

par **tize** » 08 Juil 2007, 21:17

A ma connaissance on peut montrer cela en montrant d'abord que toute matrice de trace nulle est semblable à une matrice n'ayant que des zéros sur la diagonale...

par **Ledescat** » 08 Juil 2007, 21:23

Bonsoir.
En effet! J'avais écrit ça après avoir vu la phrase dans un exo du même type disant "soit T le sev de Mn(R) engendré par les matrices AB-BA". :hein:

Oui en fait j'étais à côté de la plaque, c'est un sev engendré, donc par comb linéaires

...

par **Sylar** » 08 Juil 2007, 21:34

Et tu fais comment pour calculer le rang Rain ?

par **achille** » 09 Juil 2007, 09:51

Sylar a écrit:Et tu fais comment pour calculer le rang Rain ?

On n'a jusque là qu'un intuition que le rang devrait être n^2-1, reste à le démontrer.... :triste:

par **Sylar** » 09 Juil 2007, 10:39

Pour calculer la dimension du noyau ,je calcule le noyau:
f(X,Y)=0 => X.Y=Y.X

Ou :X appartenant a Mn(R) et Y appartenant a Mn(R) ....

Et : X=(x_ij) ou: (i,j) e [1...n]x[1...n]
Y=(y_ij)

Et : X.Y=Sum(k=1..n)[x_ik.y_kj] ; Y.X=Sum(k=1..n)[y_ik.x_kj]

==> Sum(k=1..n)[x_ik.y_kj]=Sum(k=1..n)[y_ik.x_kj]

==> Sum(k=1..n)[{x_ik.y_kj}-{y_ik.x_kj}]=0

==> x_ik.y_kj=y_ik.x_kj

Ensuite je suis bloqué....

par **tize** » 09 Juil 2007, 10:48

Bonjour,
j'ai retrouvé la référence : Exercice 6 du chapitre III p.124 (X. GOURDON Algèbre)

par **alaska** » 09 Juil 2007, 11:05

si tu veux le resoudre de maniere "standing" comme on dit chez nous
tu montre qu'il existe une base B tel que M ait sa diagonale identiquement nulle (par recurrence toute bete)
puis tu prend f(M)=DM-MD ou D est diag d'ordre n
tu montre que ker f= M/ di.mi,j=mi,j.dj
en prenant les di distinct deux a deux tu obtient mii=0
Im(f) est l'ensemble des matrices de diagonale nulle (par inclusion puis egalité des dimensions grace a l'utra classique theoreme du rang)
enfin tu conclues
voili voilou

NB:les PC sont nos amis il faut les aimer aussi

Trace nulle

trace nulle

Qui est en ligne