Les matrices dont la trace est nulle.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 21 Avr 2008, 18:03
par rifly01 » 21 Avr 2008, 18:03
Bonjour,
J'ai, encore, un petit exercice dont je ne vois pas la fin ...
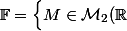\mbox{ tel que } \mbox{tr}\Big(M\Big)=0 \Big\})
1. Montrer que c'est un sev de
)
,
2. Déterminer une base de
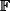
.
3. Compléter la base
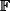
en une base de
)
.
Ce que j'ai fait :
1. C'est fait.
2. Une matrice de
)
dont la trace est nulle est de la forme

.
Par suite, une base de
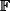
est

3.
\Big)=2^2=4)
et une base de
)
est

. Par contre, je ne vois pas comment faire pour compléter la base de
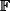
pour obtenir une base de
)
.
Et aussi, j'aimerai avoir une petite idée pour le cas de
)
.
Merci beaucoup.
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 21 Avr 2008, 18:28
par rifly01 » 21 Avr 2008, 18:28
Ah ok,
Il suffit alors d'ajouter l'élément
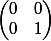
à la base de F.
Ha, ca me rappelle quelque chose. (Le clic vient de la dimension). C'est un hyperplan. Donc kerf=F (f : X--> trX).
C'est bon ?
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
 par rifly01 » 21 Avr 2008, 18:50
par rifly01 » 21 Avr 2008, 18:50
C'est vrai, on a fait ça. C'était en TD.
Merci !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
