Endomorphisme de rang 1 et trace nulle

[peperoncino]

Bonjour,

Je suis en difficulté par rapport à une question d'un exercice.
Nous avons u, un endomorphisme de rang 1.

Or, Tr(u)=0, il faut montrer que u^2=0.

Pourriez vous m'aider svp ?

[vejitoblue]

si u est endomorphisme de E de dimension n
je pense qu'on peut voir la matrice de u avec des 0 partout sur la diagonale (thm du rang => keru=n-1), n-1 zéro (valeur propre) sur la diagonale + le dernier coeff diagonal zéro (parce que tr=0). et toutes les lignes avec des zéros sauf une. du coup A² =0

c'est peut être mal dit

[Archytas]

Une autre méthode en reprenant l'idée de vejitoblue est de constater qu'effectivement toutes les valeurs propres sont nulles et donc que le polynôme minimal de est de la forme (ou caractéristique comme tu préfères, il faut juste un polynôme annulateur de cette forme donc le minimal est le plus naturel). Il y a deux possibilités :
1) Soit et donc .
2) Soit
Dans le premier cas on peut montrer que ce qui est absurde puisque 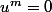. Donc on est dans le deuxième cas i.e donc ...
La méthode de veji est biens plus simple mais autant avoir plusieurs cordes à son arc .

[Pseuda]

La solution de vejitoblue dite autrement.

Ker u est de dimension n-1 (th. du rang). Dans une base de E adaptée à Ker u : (e1, ... , en-1, en), on a : u(e1)=...= u(en-1)=0. La matrice de u dans cette base comporte n-1 premières colonnes nulles, et la dernière colonne a un zéro sur la diagonale (du fait de la trace nulle de la matrice indépendante de la base). Donc u(en) est C.L. des (n-1) premiers vecteurs de la base, ainsi u²(en)=0, et comme u²(e1)=...=u²(en-1), donc u²=0.

[peperoncino]

Bonjour,
Merci à tous pour vos réponses.
Ce que je n'ai pas compris Pseuda, c'est pourquoi u(e1) =u(en-1)=0 ?

[Pseuda]

Bonjour,
Merci à tous pour vos réponses.
Ce que je n'ai pas compris Pseuda, c'est pourquoi u(e1) =u(en-1)=0 ?

(e1, ..., en-1) est une base de Ker u (à laquelle on ajoute en pour faire une base de E), donc u(e1)=...=u(en-1)=0.