Topologie quotient

[barbu23]

Bonjour :
Soient un espace topologique, une relation d'équivalence sur , et la surjection canonique, est muni de la topologie quotient de par .

Montrer que si est séparé, le graphe de est fermé dans .
Si l'on suppose ouverte ( i.e : ouverte ), établir la réciproque.
P.S : Il reste encore d'autres questions à poser, mais on fait d'abord ça !! après on passe à la suite !!
Merci d'avance de votre aide !

[barbu23]

Pour , il faut montrer que le complemntaire est ouvert :
Soit
Mais que veut dire ? que n'est pas en relation avec ? c'est ça ?

[tize]

Bonjour,
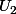
oui montrons que le complémentaire de est ouvert. Soit tel que donc . Puisque est séparé il existe des ouverts et de tels que et et .
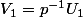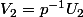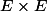
Soit alors et , on a alors ; reste à comprendre pourquoi est un ouvert de qui est inclus dans le complémentaire de .

[ThSQ]

C'est quoi le graphe d'une relation d'équivalence ?

Si est la proj canonique, il faut que classe classe réduite à un point soit fermé (condition nécessaire de séparation), il faut que soit aussi fermé, c'est-à-dire que les classes d'équivalence soient fermées. Je sais pas si ça répond à la question.

[tize]

C'est quoi le graphe d'une relation d'équivalence ?

Salut ThSQ,
je pense qu'il s'agit de

[ThSQ]

Ah ok, merci Tize. J'ai répondu à côté ....

[barbu23]

Bonjour,

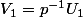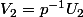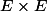
Soit alors et , on a alors ; reste à comprendre pourquoi est un ouvert de qui est inclus dans le complémentaire de .

Par définition de la topologie quotient ! donc l'image inverse d'un ouvert de la topologie qutient est un ouvert de la topologie de l'espace de depart ici c'est .. la même chose pour .. donc est un ouvert elementaire de
Pourquoi il est dans le complementaire de parcque si on prend un couple , il n'est pas dans le graphe de , c'est à dire n'est pas en relation avec .. c'est bien ça ?
Merci en tous cas !!

[legeniedesalpages]

salut,

oui enfin, je dirai plutôt pour montrer que est dans le complémentaire de que

si on prend un couple ,

on a et donc .

[barbu23]

Pour , je sais pas conclure :
Soient tel que
Alors : n'est pas en relation avec .




Puisque est ouvert, il existe des ouverts de tel que :

ouvert et ouvert. ( car est ouvert )
Il reste maintenant à justifier pourquoi .. et là je sais pas comment terminer !!
Supposons : .. alors tel que : et .. et après ?!
Merci d'avance de votre aide !!

[barbu23]

Donc ça veut dire que coupe la bissectrice !! c'est à dire c'est à dire que : ( contradiction ) c'est ça ?
Merci d'avance !!

[barbu23]

Voiçi la partie :
On suppose compact.
Démonstrer l'équivalence des propriétés suivantes :
est fermé dans est est fermée.
est une application propre.
est séparé .
Démontrer que si c'est conditions sont réalisés, est compact.
Merci d'avance !!

[barbu23]

est propre veut dire que l'image inverse d'un compact par l'application continue est un compact !

[barbu23]

T'es là "legeniedesalpages" ?

[barbu23]

Help pls !! :help:

[ThSQ]

Je vais relire calmement la topologie quotient demain (là je viens d'user mes derniers neurones sur un exo d'olympiade) mais il y a déjà une implication évidente : si b) alors E/R est compact comme image continue d'un compact.

[barbu23]

comment faire pour ?
Merci d'avance !!

[legeniedesalpages]

désolé, j'étais en train de manger, souvent je suis connecté mais je ne suis pas forcément là, je ferme mon navigateur une fois tous les deux mois quand je redémarre mon pc, et j'accumule les onglets, je les ferme jamais non plus, :lol:

Pour ton problème je regarderai ça des que je finis ma feuille d'algèbre,
là a priori en réfléchissant vite fait je saurai pas quoi te dire,
je participerai à la recherche de la solution si tu n'as pas eu plus d'indications de la part des autres collègues.

D'ailleurs je ne t'ai jamais vu posté un problème d'algèbre, toujours de la mesure ou de la topo, t'es un crack en algèbre ou vous avez pas d'algèbre dans ta fac? (si d'ailleurs il me semble que tu m'avais dit que tu faisais la théorie des groupes).

[barbu23]

Non, cette semestre on n'a que du calcul differentiel, theorie de la mesure, programmation linéaire, et topologie !! donc pas d'algèbre !! mais j'adore l'algèbre, surtout l'algèbre linéaire !!
Pour la theorie des groupes, on l'a fait quant j'étais en 2ême année de la fac !! et je me rappelle bien un peu de ce cours là !! la dernière chose qu'on a vu c'était les groupes abeliens finis !! mais, maintenant, j'ai pas le temps de revoir ça !!
j'ai un examen jeudi prochain en topologie !! je maitrise bien le cours sur les compacts et les connexes et c'est dans ces deux chapitres qu'on aura le controle !! et j'aimerai bien que quelqu'un m'aide un peu à resoudre ces exercices là !! c'est pour apprendre à demontrer et à raisonner !! c'est ça l'examen !! ils donnent pas des choses difficiles , mais il faut etre prêt à tout !!

[barbu23]

Help pls !! :hum: :help: :cry:
Merci d'avance !!

[Badra Alou]

Bonjour tout le monde.
J'ai beaucoup de probleme avec la topologie, surtout comment trouver la topologie d'un ensemble donner.
Par exemple, l'ensemble adhérence de N, avec F une famille de partie de l'adhérence telle que A appartient à F ssi A est une partie finie ou A contient +l'infini.
NB: Comment ituliser les terme mathematique avec mon ordi?
Merci les amis