Topologie : notion de densité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Balabyss
- Membre Naturel
- Messages: 14
- Enregistré le: 21 Mai 2017, 11:07
-
 par Balabyss » 05 Nov 2017, 16:36
par Balabyss » 05 Nov 2017, 16:36
Bonjour, Bonsoir a tous, je reviens vous voir avec une question qui me taraude encore et toujours, j'étais en train de faire un exercice sur les espaces topologiques quand je suis tombée sur cette question :
Soit
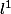
= {
_{k\in N}\in R^{n} | \sum_{k=0}^{\infty }{|x_{k}| converge}})
}
un espace vectoriel normé et Pour tout
_{k\in N}\in l^{1})
on notera :

Soit E un sous espace vectoriel de
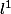
définie de la sorte :
E={
_{k\in N})
| Il existe

tq pour tout

}
Montrer que E est dense dans
)
Voila voila ! merci beaucoup pour votre aide >.< !
Modifié en dernier par
Balabyss le 05 Nov 2017, 17:13, modifié 1 fois.
-
Mimosa
- Membre Relatif
- Messages: 432
- Enregistré le: 19 Aoû 2016, 16:31
-
 par Mimosa » 05 Nov 2017, 16:43
par Mimosa » 05 Nov 2017, 16:43
Bonjour
Il manque quelque chose dans ton énoncé. Un sous-espace quelconque (par exemple une droite) n'a aucune raison d'être dense!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Nov 2017, 16:45
par Ben314 » 05 Nov 2017, 16:45
Salut,
Balabyss a écrit:Soit E un sous espace vectoriel de
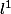
Montrer que E est dense dans
)
Faudrait peut-être songer à utiliser un peu sa cervelle de temps en temps : tu crois
VRAIMENT que si on prend un s.e.v. quelconque de
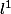
(par exemple le singleton ne contenant que le vecteur nul), ça va être dense dans
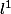
?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Balabyss
- Membre Naturel
- Messages: 14
- Enregistré le: 21 Mai 2017, 11:07
-
 par Balabyss » 05 Nov 2017, 17:09
par Balabyss » 05 Nov 2017, 17:09
Mimosa a écrit:Bonjour
Il manque quelque chose dans ton énoncé. Un sous-espace quelconque (par exemple une droite) n'a aucune raison d'être dense!
Oui en effet vue que c'est la seule question ou j'ai eu de la difficulté, j'ai oublié de préciser la nature de E, je viens de corriger ça
-
Balabyss
- Membre Naturel
- Messages: 14
- Enregistré le: 21 Mai 2017, 11:07
-
 par Balabyss » 05 Nov 2017, 17:15
par Balabyss » 05 Nov 2017, 17:15
Ben314 a écrit:Salut,
Balabyss a écrit:Soit E un sous espace vectoriel de
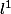
Montrer que E est dense dans
)
Faudrait peut-être songer à utiliser un peu sa cervelle de temps en temps : tu crois
VRAIMENT que si on prend un s.e.v. quelconque de
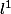
(par exemple le singleton ne contenant que le vecteur nul), ça va être dense dans
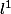
?
Non et j'en suis bien consciente, j'avais juste oublié de mentionner la nature de E.
-
aviateur
 par aviateur » 05 Nov 2017, 18:46
par aviateur » 05 Nov 2017, 18:46
Bonjour
Soit
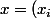)
un élément quelconque de
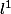
On définit la suite
}) \in l^1)
telle que
}_i=x_i)
si

et
}_i=0)
sinon.
que penses tu de la suite
}))
?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 102 invités
(par exemple le singleton ne contenant que le vecteur nul), ça va être dense dans
?