Bonjour, voilà le souci auquel je suis confronté :
On a E un espace vectoriel normé de dimension quelconque, H un hyperplan de E
On suppose que H est dense dans E et soit b appartenant à E\H
Montrer que b+H est dense dans E
Merci.
Topologie - Hyperplan - Densité
8 messages
- Page 1 sur 1
Re: Topologie - Hyperplan - Densité
Je ne sais pas s'il suffit de passer par des limites de suites, mais le résultat est alors très rapide
Re: Topologie - Hyperplan - Densité
pascal16 a écrit:Je ne sais pas s'il suffit de passer par des limites de suites, mais le résultat est alors très rapide
Oui j'y ai pensé mais en prenant la somme directe de vect(b) et H, y aura un problème avec le scalaire devant b , non ?
Re: Topologie - Hyperplan - Densité
b nul -> évident
b non nul, le vecteur b est un base de Vect(b)
J'aurais simplement décomposé un élément de E sur b + une base de H, notons cette décomposition a+h (h est un vecteur de dimension quelconque-1, vérifier les éventueles sous-cas)
il existe une suite U de H qui tend vers h
U+a tends vers l'élément choisi.
b non nul, le vecteur b est un base de Vect(b)
J'aurais simplement décomposé un élément de E sur b + une base de H, notons cette décomposition a+h (h est un vecteur de dimension quelconque-1, vérifier les éventueles sous-cas)
il existe une suite U de H qui tend vers h
U+a tends vers l'élément choisi.
Re: Topologie - Hyperplan - Densité
Salut,
Je suis pas sûr du tout que ce soit malin d'évoquer une quelconque base de H dans un cas pareil (principalement du fait que pour garantir l'existence d'une telle base, il faut l'axiome du choix . . .).
Sans compter que l'exo. est totalement trivial : si on prend un x quelconque de E, x-b est bien évidement un élément de E donc il existe une suite (h_n) d'élément de H qui tend vers x - b (car H est dense).
Et la suite (b+h_n) de l'hyperplan affine b+H tend vers b+(x-b)=le x de départ.
Je suis pas sûr du tout que ce soit malin d'évoquer une quelconque base de H dans un cas pareil (principalement du fait que pour garantir l'existence d'une telle base, il faut l'axiome du choix . . .).
Sans compter que l'exo. est totalement trivial : si on prend un x quelconque de E, x-b est bien évidement un élément de E donc il existe une suite (h_n) d'élément de H qui tend vers x - b (car H est dense).
Et la suite (b+h_n) de l'hyperplan affine b+H tend vers b+(x-b)=le x de départ.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Topologie - Hyperplan - Densité
perso, je n'ai pas d'exemple sous la main qui vérifie "On suppose que H est dense dans E ", je ne vois que des contres exemples.
par contre, un cheminement qui me parait plus logique :
E dense dans H, H un hyperplan de A
b dans A\H
b+E dense dans A
par contre, un cheminement qui me parait plus logique :
E dense dans H, H un hyperplan de A
b dans A\H
b+E dense dans A
Re: Topologie - Hyperplan - Densité
En dimension finie c'est pas possible : tout s.e.v. est fermé.
Par contre, si tu prend pour E l'ensemble des fonctions continues de [0,1] dans R muni de la norme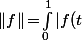|\,dt) et pour H l'ensemble des f de E telles que f(0)=0 alors H est un hyperplan dense de E (et ça vient du fait que la forme linéaire E -> R ; f -> f(0) n'est pas continue).
et pour H l'ensemble des f de E telles que f(0)=0 alors H est un hyperplan dense de E (et ça vient du fait que la forme linéaire E -> R ; f -> f(0) n'est pas continue).
Et dans ce cas, un hyperplan affine b+H du type de celui dont parle l'exo., c'est l'ensemble des f de E tels que f(0)=cst pour une constante fixé.
Par contre, si tu prend pour E l'ensemble des fonctions continues de [0,1] dans R muni de la norme
Et dans ce cas, un hyperplan affine b+H du type de celui dont parle l'exo., c'est l'ensemble des f de E tels que f(0)=cst pour une constante fixé.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
