Un théorème sur la théorie des groupes.

[Georges10]

Bonsoir à tous.
Svp il y'a un théorème que je ne comprend pas bien. C'est celui-ci :
Soit (G,*) un groupe. (H,*) est un sous groupe de (G,*). Il existe une bijection entre l'ensemble des classes à gauche et l'ensemble des classes à droite.

Pour prouver ce theoreme, il faut de prime abord monter que φ : xH ---> Hx⁻¹ est une application. Pour cela, on a cherché à montrer que si ( ∀ x,y ∈ H ) xH = yH alors Hx⁻¹ = Hy⁻¹ . Ma question est de savoir en quoi est ce que cela nous permet de savoir que φ est une application.
merci d'avance!

[hdci]

Bonjour,
Une application, c'est une relation entre deux ensembles telle que tout élément de l'ensemble de départ est en relation avec un et un seul élément de l'ensemble d'arrivée.

La relation , à ce stade, n'est qu'une relation : il est clair que existe, il faut s'assurer qu'il est unique.

Or il y a plusieurs façons d'écrire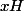 (surtout si H n'est pas le sous-groupe trivial). Considérons alors tel que 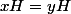. D'après la définition de la relation, 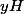est associé à , par suite 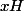est associé à et à .
Donc s'il existe tel que 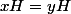, mais la relation ne serait pas une application car il y aurait plusieurs images pour .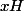

D'où en démontrant , on montre l'unicité de l'image et il s'en suit que est une application.

[Georges10]

Ah d'accord, merci beaucoup, je comprend mieux. Passez une bonne soirée !