Théorème de Rolle

[alecs20]

Merci a ceux qui viennent de me répondre pour l'autre post. Je viens de voir une autre question que je n'arrivais pas a résoudre:

Démontrer qu'entre deux racines réelles de (e^x)sinx = 1, il existe au moins une racine réelle de (e^x)cosx = -1. Il faut utiliser le théorème de Rolle pour y répondre.

[mathador]

Salut,

posons , il faut d'abord démontrer que f admet au moins 2 racines réelles distinctes, sinon l'énoncé perd son sens et son intérêt.

Partant de a < b racines distinctes consécutives (les autres cas s'en déduisent trivialement) de f, on a f(a) = f(b) = 0 ; on nous dit d'utiliser Rolle, donc assurons-nous que f est continue sur [a,b], dérivable sur ]a,b[.

Une fois ce travail fait, le théorème nous dit qu'il existe c entre a et b où la dérivée f ' de f s'annule ; quelle est l'expression de cette fonction dérivée ? Comment peut-on travailler la pâte ? il va falloir faire apparaître du , je te laisse chercher (j'avoue que je pense que c'est la méthode, mais je ne me suis pas donné la peine de finir le travail pour vérifier, donc si tu bloques ne t'affolles pas, j'ai peut-être mal senti le coup !)

Bon courage !

[aviateurpilot]

c'est ce que j''ai fait
mais on trouvé pas la solution
c'est pour cela que j'ai pas posté cette methode mathador

[mathador]

Merci de ta vivacité Aviateurpilot. Si le problème est plus compliqué qu'il n'y paraît, je vais chercher du papier et un crayon !!!

[mathador]

Héhéhé, trop drôle ... c'est vrai que ça bloque bien ... il faut poser une autre fonction, c'est ça le truc. Laquelle, c'est la vraie question !!!! le devoir m'appelant, je m'arrête là en laissant Alpha y réfléchir, car je sais qu'il se creuse les méninges !

[alecs20]

e^(-x) - sinx peut-etre?? (En réponse a mathador)

[Yipee]

Une méthode peu élégante mais efficace est de voir que les racines de sont très proches des racines de 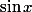et celles de proches de celles de .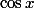

Ce n'est pas très beau - et cela n'utilise pas Rolle - mais cela marche. Sinon je pense comme mathador que l'on doit appliquer Rolle à ce qui permet de trouver un nombre c compris entre a et b qui est une racine de . A ce moment si on suppose que f est au dessus de 1 sur on a que . Puis...

[mathelot]

l'équation équivaut à

l'équation équivaut à

et on applique Rolle. ah,oui, c'est ce qu'avait trouvé alecs20.

[alecs20]

Donc, si j'ai bien compris:

Soit , que nous pouvons ramener a . Il existe faisant partie des réels, (en supposant 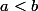... ou le contraire), avec cette fonction continue sur [a,b] et dérivable sur ]a,b[. Il existe donc aussi faisant partie des réels, tel que . Si nous dérivons , nous obtenons , et nous en déduisons . CQFD.

c'est bon? Ou j'aurais du rajouter de quoi?

[Alpha]

Oui, c'est bon, tu multiplies juste la dernière égalité par e^x, et d'après ce que tu viens de dire, il existe c, ...