Theoreme de Rolle
7 messages
- Page 1 sur 1
Theoreme de Rolle
Bonjour a tous,je suis etudiant en 1er année de license de phisique chimie science pour l'ingénieur et pour conclure ce premier semestre nous devons traiter un sujet de communication scientifique.Mon sujet est exposer quelques généralisation du théoréme de Rolle:cas d'une fonction définie sur une intervalle borné et ouvert,fermé et non borné... Le probléme c'est que ce la premiére fois que je vois le théoréme en question et je ne le maitrise pas totalement.Si quelqu'un pourrai me donner quelque petit conseil sur l'etablissement d'un sujet de communication scientifique ainsi qu'un petit coup de main pour bien comprendre le theoreme de Rolle je lui serai trés reconnaissant et je doit rendre mon devoir pour le 23/01 alors faite vite s'il-vous-plait je vous remercie d'avance
Rolle généralisé à 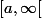 .
.
Soit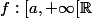 continue sur
continue sur 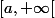 et dérivable sur
et dérivable sur 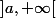 . On suppose que
. On suppose que = \lim_{x\to +\infty } f(x)) . Alors il existe un réel c>a tel que f'(c)=0.
. Alors il existe un réel c>a tel que f'(c)=0.
Démonstration.
Si f est constante c'est trivial.
Sinon soit b>a tel que\neq f(a)) .
.
Supposons par exemple f(b)>f(a).
On pose+f(b)}{2}) .
.
On applique le théorème des valeurs intermédiaires sur [a,b] : m=f(u).
De même on peut l'appliquer sur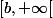 . En effet
. En effet  = \lim_{x\to +\infty }f(x)) , donc il existe un réel e > b tel que f(e) b tel que f(v)=m.
, donc il existe un réel e > b tel que f(e) b tel que f(v)=m.
On a donc u<v et f(u)=f(v). On peut appliquer le théorème de Rolle f'(c)=0 pour un réel c de [u,v].
Soit
Démonstration.
Si f est constante c'est trivial.
Sinon soit b>a tel que
Supposons par exemple f(b)>f(a).
On pose
On applique le théorème des valeurs intermédiaires sur [a,b] : m=f(u).
De même on peut l'appliquer sur
On a donc u<v et f(u)=f(v). On peut appliquer le théorème de Rolle f'(c)=0 pour un réel c de [u,v].
Salut jaysean02
Pour ton papier tu pourrais t'inspirer de la thèse de Jean Dieudonné, un peu ancienne mais vu l'aura de l'auteur ça devrait passer.
Pour mémoire :
Recherches sur quelques problèmes relatifs aux polynomes et aux fonctions bornées d'une variable complexe. Paris, Gauthier-Villars, 1931
Je crois me souvenir qu'un chapitre traite de la généralisation du théorème de Rolle aux fonctions à variables complexes.
Pour ton papier tu pourrais t'inspirer de la thèse de Jean Dieudonné, un peu ancienne mais vu l'aura de l'auteur ça devrait passer.
Pour mémoire :
Recherches sur quelques problèmes relatifs aux polynomes et aux fonctions bornées d'une variable complexe. Paris, Gauthier-Villars, 1931
Je crois me souvenir qu'un chapitre traite de la généralisation du théorème de Rolle aux fonctions à variables complexes.
Salut BDdupont
La thèse de Dieudonné... hum hum . Rien que ça?
Je peux affirmer sans risque de me tromper que tu ne trouveras pas une goutte accessible au niveau licence là-dedans.
Plus basique sur le sujet que tu évoques, il y a le théorème de Gauss-Lucas qui dit que les racines de P'(z) sont dans l'enveloppe convexe des racines de
P(z). Dans R c'est bien un cas particulier de Rolle qui dit qu'entre deux racines de P(x), il y a une racine de P'(x).
La thèse de Dieudonné... hum hum . Rien que ça?
Je peux affirmer sans risque de me tromper que tu ne trouveras pas une goutte accessible au niveau licence là-dedans.
Plus basique sur le sujet que tu évoques, il y a le théorème de Gauss-Lucas qui dit que les racines de P'(z) sont dans l'enveloppe convexe des racines de
P(z). Dans R c'est bien un cas particulier de Rolle qui dit qu'entre deux racines de P(x), il y a une racine de P'(x).
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
