Bonjour à tous,
Nous avons prouvé en cours de calcul différentiel une version "faible" du théorème du rang constant :
Soit

de classe

et soit
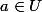
tel que

soit surjective. Alors, il existe un voisinage ouvert de


, un ouvert
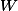
de

et un difféo

tels que
 = (x_1,...,x_m))
.
Pour prouver cela, on commence par dire que, comme la différentielle en

est de rang

, on peut, quite à remplacer

par

(où

est un automorphisme de
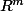
et

un automorphisme de

), supposer que la jacobienne de

en

est de la forme

où
)
est inversible et où
)
(ce qui revient à faire un changement de base au départ et à l'arrivée).
Ensuite, on prouve le théorème dans ce cas (pas de problème à ce niveau là).
Simplement, je ne comprends pas comment se ramener ensuite au cas d'une fonction

"quelconque" (i.e. sans cette simplification).
Si je pose

, alors, le théorème est prouvé pour
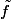
. J'ai donc un voisinage
})
de
)
, un ouvert
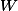
de

et un difféo
})
tel que
= (x_1,...,x_m))
. En posant

et
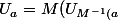}))
(voisinage ouvert de

car

automorphisme), j'ai un difféo

(car un automorphisme est aussi un difféo et que la composée de deux difféos est encore un difféo) tel que
 = (x_1,...,x_m))
. Mais comment se débarrasser du

?
Le problème de ce genre de simplification, c'est qu'à chaque fois on écrit "quite à remplacer truc par machin, on suppose que ...", sans jamais détailler comment on se ramène au cas général... Du coup je pense que de toute ma scolarité je n'ai jamais vu ce genre de choses rédigée "proprement"


