Je vais y aller par petit bouts (i.e. je rallongerais au fur et à mesure).
(A) Le théorème d'algèbre linéaire dont je parle, il est totalement élémentaire et tu l'a obligatoirement vu.
Si tu as une application linéaire
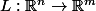
de rang

, tu as (par définition)
\big)\!=\!r)
donc il existe une base
)
de
)
que tu peut compléter en une base
)
de
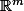
.
Vu que, pour tout
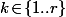
, on a
)
, il existe
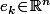
tel que
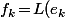)
.
Posons aussi
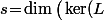\big))
et considérons une base
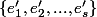
du noyau
)
.
SI on prend maintenant un
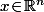
quelconque, vu que
\!\in\!\text{Im}(L))
il s'écrit (de façon unique)
\!=\!\lambda_1 f_1\!+...+\!\lambda_r f_r\!=\!L(x'))
où
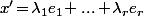
et, comme
)
c'est que
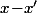
s'écrit (de façon unique)
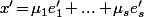
. Donc
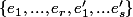
est une base de
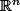
.
Ca signifie en particulier que
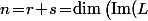\big)\!+\!\dim\big(\ker(L)\big))
(*)
Mais ça signifie aussi que, dans les bases
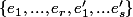
de
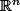
et
)
de
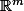
, la matrice de

est (par construction)

.
(*) Et ça, tu l'a obligatoirement vu : ça fait parti des théorème "de base" de l'algèbre linéaire et c'est pour ça que je disait au début que le résultat en question, tu l'a forcément déjà vu. Mais c'est vrai que souvent, on ne mémorise que la partie du résultat qui parle des dimensions du noyau et de l'image et on "oublie" ce que ça dit en terme de matrices.
(B)
goupil59 a écrit:Soit

des ouverts et

de classe
)
. Soit
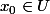
tel que
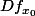
est de rang
)
. Alors, il existe un voisinage
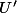
de

dans

, un voisinage
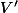
de
)
dans

et deux difféomorphismes

tels que
 = \textcolor{red}{(y_1,...,y_r,0,...0)})
.
Ca, c'est encore plus incohérent qu'avant : non seulement tu n'a pas réglé le "problème" consistant à voir qu'il n'y a aucune raison qu'il y ait des vecteurs de la forme (?,...?,0,...0) dans l'ensemble d'arrivé
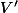
de
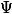
, mais en plus ça n'a plus de sens vu qu'on sait pas du tout ce que représente les

là dedans. Tant qu'on avait que des

dans la formule, on pouvait considérer que la formule constituait un "abus de langage" (fréquent), c'est à dire que,
écrite correctement, elle aurait du être précédée d'un
\!\in\!U')
, mais si tu met aussi des

sans préciser d'où ils sortent (ou comment ils sont quantifiés), ben là, c'est plus un simple "abus de langage" : c'est du "grand n'importe quoi".
Et s'il faut le comprendre sous la forme
\!\in\!U',\ \exists(y_1,...,y_r)\!\in\!{\mathbb R}^n\text{ t.q. }\cdots})
alors non seulement ça reste faux (à cause du 1er argument çi dessus), mais même si c'était vrai, je pense que ça n'aurais aucun intérêt comme théorème vu le "peu" que ça dit (aucune méthode "calculatoire" expliquant comment on obtient les

partant des

)
(C)
goupil59 a écrit:Etape 1 : =\Pi(x_1,...,x_n))
où
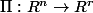
projection canonique.
On considère l'application
=(\Pi \circ f(x_1,...,x_n), x_{r+1},...,x_n])
Sa différentielle est
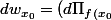} \circ df_{x_0}, Id_{n-r}) = (\Pi ^2 , I_{n-r}) = Id_n)
Puisque
=1 \neq 0)
, par le théorème d'inversion locale, il existe un ouvert
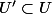
contenant

et un difféo
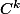
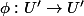
tel que
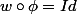 (là, j'ai quand même un doute sur le fait que l'on ait bien
(là, j'ai quand même un doute sur le fait que l'on ait bien 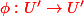 ).
).
Et tu as raison (de douter) : la fonction

, elle envoie le vecteur

sur le vecteur
)
dont les premières

coordonnées sont celles de
)
et les dernières sont celles de

. Et comme ce vecteur, il y a aucune raison qu'il soit égal à

, la fonction

n'envoie sûrement pas un voisinage de

sur lui même (et donc sa bijection réciproque locale non plus)
Je pense que je vais m’arrêter là : le reste, c'est du même tonneau : les "idées", c'est évidement les bonnes (= utiliser le théorème d'inversion locale), mais par contre y'a la moitié des ensemble de départ ou d'arrivé dont il parle qui sont complètement faux et ces histoires de matrices en bloc, c'est évidement systématiquement "à permutation des bases prés" (voir l'exemple de mon premier post).
Sans parler du fait que, si tu n'écrit "que" ça :
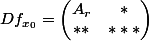
avec
\neq 0)
Sans aucune précision concernant les propriétés des sous matrices * ; ** et ***, c'est assez clair que ça va merder dans la suite vu que tu as uniquement traduit que le rang est
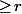
et pas qu'il est


 ). Effectivement, les énoncés (et les preuves) trouvés sur internet ou dans des livres se rapprochent beaucoup plus de ce que tu énonces toi. Cependant, dans le reste de la preuve (que je pensais avoir comprise, du moins jusqu'aux trois-quarts...), lors de la "construction" des difféomorphismes, aucune mention n'est faite d'un voisinage de 0. J'aimerais quand même comprendre où se situe l'arnaque là dedans... J'ai quelques doutes à certains endroits de la preuve, mais je ne sais pas trop comment corriger les erreurs (s'il y en a)...
). Effectivement, les énoncés (et les preuves) trouvés sur internet ou dans des livres se rapprochent beaucoup plus de ce que tu énonces toi. Cependant, dans le reste de la preuve (que je pensais avoir comprise, du moins jusqu'aux trois-quarts...), lors de la "construction" des difféomorphismes, aucune mention n'est faite d'un voisinage de 0. J'aimerais quand même comprendre où se situe l'arnaque là dedans... J'ai quelques doutes à certains endroits de la preuve, mais je ne sais pas trop comment corriger les erreurs (s'il y en a)...